Фундаментальные основы нанонаук и компьютерный инжиниринг наносистем
Иллюстративный мультимедийный комплекс CompNano
2024 dragon

Компьютерное моделирование самосборки и самоорганизации неравновесных фрактальных наносистем металлов и неметаллов

Определение кластеров

Кластер — группировка из атомов металлов, находящихся на расстояниях, допускающих прямое взаимодействие металл-металл.

Фрактальный кластер — кластер, плотность числа частиц которого с увеличением расстояния от центра роста убывает по закону, описываемому показателем в соотношении число частиц–радиус.

Плотность числа частиц на радиусе r для кластеров определяется выражением:

\rho(r)\approx&space;R_0^{-D}r^{D-E}, (1)

где R0 — характерный минимальный размер (размер атома либо молекулы),
D — фрактальная размерность
Е — евклидова размерность, в которой находится кластер.

Плотность постоянна при условии D = E.

Кластеры металлов

На рисунках представлены примеры структур атомных кластеров никеля с минимальной энергией связей, а также примеры конфигураций двухмерного и трёхмерного фрактальных атомных кластеров никеля.

Структура атомных кластеров никеля с минимальной энергией связей
Структура двухмерного и трёхмерного фрактальных атомных кластеров никеля

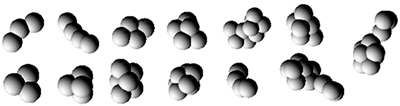
Неравновесные условия синтеза приводят к образованию фрактальных кластеров, которые являются неустойчивыми к внешним воздействиям. Распадаясь под действием тех или иных факторов, фрактальные кластеры образуют островковые структуры (см. также [3]).

Компьютерное моделирование

Объектами данного обсуждения являются системы атомов никеля, состоящие из сотен атомов, и являющиеся фрактальными нанокластерами либо островковыми системами в зависимости от условий моделирования.

Моделирование — исследование объектов познания на их моделях, построение моделей реально существующих предметов, явлений или процессов.

Наиболее активно используемыми в молекулярной нанотехнологии методами молекулярного моделирования являются:

  • метод молекулярной механики;
  • метод молекулярной динамики;
  • метод Монте-Карло.

Моделирование самоорганизации наносистем

Комплекс «Компьютерная нанотехнология» включает в себя модуль «Нанотрансформеры», который позволяет моделировать формирование наносистем атомов в изохорно-изотермических условиях.

Спонтанное зарождение островковых наноструктур при росте плёнок из пара описывается рядом элементарных процессов:

  1. адсорбция;
  2. поверхностная диффузия;
  3. образование зародышей;
  4. рост зародышей.

Устойчивые зародыши являются эффективными стоками для атомов двумерного газа, и при определённой плотности этих стоков вероятность захвата ими одиночных адсорбированных атомов превышает вероятность реиспарения, вследствие чего не образуется новых стабильных центров роста.

Одними из возможных формируемых островковых наноструктур могут быть фрактальные кластеры и структуры их временной эволюции.

В рамках модели выделено две стадии самоорганизации наноструктуры из атомного двумерного газа:

  1. поатомная самосборка структуры по алгоритму ограниченной диффузией агрегации (ОДА);
  2. преобразование структуры по алгоритму «наискорейшего спуска» по поверхности потенциальной энергии.

Алгоритмы модели ОДА

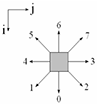
Направление перемещения частицы в соответствии со случайно сгенерированным числом

В основе алгоритмов ОДА моделирования лежат два двумерных массива: na(i, j) и a(i, j). Двумерный массив a(i, j) соответствует текущему временному шагу, а двумерный массив na(i, j) соответствует будущему временному шагу.

В первоначальный момент времени размещается центр агрегации с координатами (i, j) и случайным образом распределяются диффундирующие частицы с заданной концентрацией.

Каждая из диффундирующих частиц на последующем временном шаге занимает своё положение в одной из восьми соседних клеток в зависимости от того, какому интервалу принадлежит вероятность, генерируемая оператором случайных чисел: 

c: p = Round(Rnd*8)
If p = 8 Then GoTo c

При этом накладываются дополнительные правила: частицы могут перемещаться только в те ячейки, которые не заняты как на данном временном шаге, так и на последующем.

Окрестность Мура

Если та клетка, в которую должна переместится данная частица, занята, то идёт пересчёт вероятности, пока не определится свободное направление движения. Если у частицы нет свободного направления, то она остаётся на своём месте. Эти условия устраняют наслоение перемещающихся частиц друг на друга.

Каждая блуждающая частица становится частью растущего нанодендрита при попадании её в окрестность Мура.

Процесс продолжается до тех пор, пока кластер не будет содержать заданное число агрегированных частиц или до агрегирования всех частиц системы.

На рисунке представлен кластер, синтезированный при концентрации 10% и размере области 100×100 клеток.

Рост дендритов возникает потому, что атомы необходимые для роста, диффундируют извне и удаляется тепловая энергия [1].

Детальнее ознакомиться с реализацией алгоритмов самосборки и релаксации фрактальных нанокластеров никеля слушатели курса смогут при выполнении практической работы «Дизайн и проектирование самосборки и самоорганизации нанокластеров с помощью модуля “Нанофракталы”» .

Энтропия системы атомов

Энтропия системы блуждающих и агрегированных атомов рассчитывалась через термодинамическую вероятность из следующего соотношения.

S=k_B\ln\frac{N!}{\prod_{i=1}^{q}N_i!}, (2)

где q — число ячеек; N — общее число атомов; Ni — число атомов в i-той ячейке.

Энергия связей и энергия Гельмгольца

В адиабатическом приближении внутренняя энергия наносистемы n атомов определяется профилем поверхности потенциальной энергии (ППЭ) в конфигурационном пространстве ядер, как сумма отдельных адиабатических энергий электронных связей:

E=\sum_i^n\sum_j^n&space;S_{ij}\varepsilon_{ij}(R_{ij}), (3)

где Sij — матрица смежности; εij — энергия связи; Rij — длина связи.

Адиабатическая энергия связи пары атомов может быть аппроксимирована функцией, выраженной в виде потенциала Морзе:

\varepsilon_{ij}(R_{ij})=D_0\left[\exp(-2\alpha(R_{ij}-R_0))-2\exp(-\alpha(R_{ij}-R_0))\right]. (4)

Можно выделить факторы, которые определяют эволюцию системы во времени:

  1. алгоритмы перемещения атомов;
  2. радиус захвата атомов при образовании химической связи;
  3. изменение энтропии системы;
  4. температура;
  5. изменение свободной энергии системы.

Следует заметить, что температура определяет как радиус захвата Rкрит, так и связанную энергию TΔS.

В системе конкурируют два фактора: энергетический и энтропийный.

Критерий термодинамической устойчивости системы с фиксированными температурой и объёмом — минимум свободной энергии. Свободная энергия системы рассчитывается через значения внутренней энергии, энтропии и температуры из следующего выражения:

F=E-TS. (5)

Вычисление фрактальной размерности

Важной количественной характеристикой фрактала является фрактальная размерность. Знание фрактальной размерности, наряду с другими свойствами рассматриваемого фрактала, позволяет предсказать расчётным путём ряд особенностей его поведения, не проводя опытных исследований. В настоящее время существует много способов расчёта данной величины. Рассмотрим здесь метод определения клеточной фрактальной размерности.

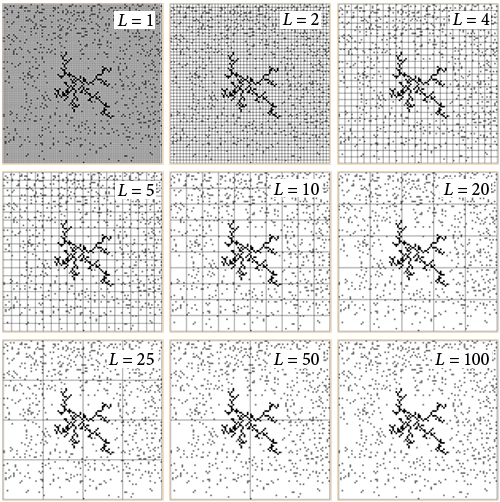
Фрактальная размерность системы рассчитывалась методом наложения сеток в соответствии со следующим выражением:

N(L)=\frac{b}{L^D}, (6)

где L — длина ячейки в сетке; D — фрактальная размерность; N — число занятых ячеек в сетке; b — константа.

На рисунке приведён пример вычисления фрактальной размерности системы атомов в области 100×100 клеток.

Список ремомендуемой литературы

  1. Тоффоли Т. Машины клеточных автоматов / Т. Тоффоли, Н. Марголус; пер. с англ. П.А. Власова, Н.В. Барабанова; под ред. Б.В. Баталова. – М.: Мир, 1991. – 278 с.
  2. Трусов Л.И., Холмянский В.А. Островковые металлические плёнки. – М.: Металлургия, 1973
  3. Brechignac C. Thermal and chemical nanofractal relaxation / C. Brechignac, Ph. Cahuzac, F. Carlier, C. Colliex, M. de Frutos, N. Kebaili, J. Le Roux, A. Masson, B. Yoon // Eur. Phys. J. – 2003. – D24. – P. 265–268.
  4. Монокристаллические плёнки / пер. с англ. С.Н. Рорина, А.К. Милой, А.Ф. Орлова; под ред. проф., д-ра хим. наук З.Г. Пискера. – М.: Мир, 1966
  5. Буркерт У. Молекулярная механика / У. Буркерт, Н.Л. Эллинжер; пер. с англ. В.С. Мастрюкова. – М.: Мир, 1986. – 364 с.
  6. Комник Ю.Ф. Физика металлических плёнок. Размерные и структурные эффекты. – М.: Атомиздат, 1979
  7. Домрачев Г.А. Роль углерода и металла в самоорганизации системы железо-углерод при различном содержании компонентов / Г.А. Домрачев, А.И. Лазарев, Б.С. Каверин, А.Н. Егорочкин, А.М. Объедков, Е.Г. Домрачева, Л.Г. Домрачева, Г.В. Маркин, E. Huipe Nava, А.А. Сорокин, О.Н. Суворова, В.Л. Карнацевич, А.И. Кириллов, А.А. Закуражнов // Физика твёрдого тела. – 2004. – Т.46, вып.10. – С. 1901–1915.
  8. Губин С.П. Химия кластеров – достижения и перспективы // Журнал всесоюзного химического общества им. Д.И. Менделеева. – 1987. – Т.XXXII, №1. – С. 3–11
  9. Петров Ю.И. Физика малых частиц. – М.: Наука, 1982. – 359 с.
  10. Губин С.П. Химия кластеров. Основы классификации и строение. – М.: Наука, 1987. – 263 с.
  11. Гафнер Ю.Я. Роль температуры при изменении структуры нанокластеров Ni / Ю.Я. Гафнер, С.Л. Гафнер, Р. Мейер, Л.В. Редель, П. Энтель // Физика твёрдого тела. – 2005. – Т.47, вып.7. – С. 1304–1308
  12. Федер  Е. Фракталы / Е. Федер; пер. с англ. Ю.А. Данилова, А. Щукурова. – М.: Мир, 1991. – 260 с.
  13. Эберт К. Компьютеры. Применение в химии / К. Эберт, Х. Эдерер; пер. с нем. – М.: Мир, 1988. – 416 с.
  14. Полторак О.М. Термодинамика в физической химии / О.М. Полторак. – М.: Высш. шк., 1991. – 318 с.
  15. Мюнстер А. Химическая термодинамика / А. Мюнстер; пер с нем. Е.П. Агеева; под ред. Я.И. Герасимова. – М.: Едиториал УРСС, 2002. – 295 с.