Исследование фемтосекундной корпоративной динамики неравновесных наносистем с помощью модуля «НаноТрансформеры»

Обоснование и проблематика

Известно, что химические реакции в молекулах и в материалах, как реакции разрыва и образования химических связей атомов, происходят за счет сдвига ядер. Быстрота движения ядер характеризуется периодами их колебаний относительно положений равновесия. Реакция не может происходить за времена меньшие, чем периоды колебания ядер, поэтому они задают характерный «квант» времени химических реакций в веществе. Полное время протекания типичных элементарных химических реакций во всех веществах лежит в пределах 10–10⁴ фс. Они длятся на протяжении от одного до сотен периодов колебания ядер.

Для изучения быстрых актов реакционных процессов с конца 1980-х годов применяется фемтосекундная лазерная спектроскопия, использующая временное сжатие лазерных световых импульсов. У истоков данного направления, получившего название «Фемтохимия», стоит имя Ахмеда Зевейла, получившего в 1999 г. Нобелевскую премию по химии за исследования в области фемтосекундной спектроскопии. К тому времени в исследовании химических процессов был достигнут нижний временной предел сжатия лазерных импульсов, составлявший 4 фс.

Считается, что дальше укорачивать импульсы бессмысленно, так как даже самые быстрые элементарные химические реакции длятся больше, чем 10 фс. Предполагается, что кроме химических реакций причин дискретизации кинетики процессов в веществе нет. Так как в отсутствие химических реакций движение системы атомов и их связей описывается непрерывной эволюцией, то они теоретически исследуются компьютерным моделированием в соответствии с законами непрерывной молекулярной динамики. Однако в конце 90-х годов в рамках квантово-полевых концепций (термополевая динамика, квантово-полевая химия) конденсированного состояния были предсказаны полевые эффекты дискретизации эволюции плазмы электронов в наноструктурах вещества и в отсутствие химических реакций [1, 2]. Эффекты дополнительной дискретности кинетики наноструктурных процессов связаны с наличием в полевых плазменных системах кроме элементарных квантовых частиц ещё и временно-живущих составных квантовых частиц — компактонов (роевых пар электронов, электронов и антиэлектронов, их троек, четверок и т. д.). Теория компактонов была рассмотрена в одной из первых публикации по основам квантово-полевой химии в начале 90-х годов [1].

Цель работы: средствами компьютерного эксперимента исследовать мультикинетику дискретно-алгоритмической эволюции наносистем при свехскоростных фемтосекундных процессах обмена энергией в среде мультистабильных трансформеров.

Порядок выполнения работы

В лабораторной работе «Дизайн и проектирование самосборки и самоорганизации неравновесных наносистем» вами были исследованы стационарные неравновесные аттракторы эволюции кубических нанокластеров никеля и железа. При этом особенности задачи, связанные с временно́й и пространственной дискретизацией, хотя и подразумевались, но были оставлены фактически без внимания. Основываясь на модельном формализме идеи корпоративной стохастической эволюции неравновесных наносистем, соответствующие версии программы семейства «NanoEvolver» позволяют количественно отслеживать изменения, которые претерпевают разнообразные параметры этих наносистем, и строить разверки соответствующих величин во времени. Данная возможность доступна при включении опции, ответственной за ведение log-файла. Анализ данных log-файлов дает ценные сведения о возможно неявных процессах, происходящих на фоне общего движения наносистемы, о временах начала и завершения этих процессов, о времени достижения стационарного неравновесного состояния и т.д. Настоящая лабоаторная работа подразумевает активное использование этих возможностей при моделировании наносистемных процессов и разборе результатов такого моделирования.

К моменту перед началом выполнения лабораторной работы на вашем компьютере должна быть запущена программа «NanoEvolver» — Dissipative (версия 4.2). Если это не так, запустите программу. При необходимости расположите окно программы и окно справки на экране так, чтобы обеспечить себе удобство чтения настоящего руководства к лабораторной работе и выполнения инструкций в окне «NanoEvolver».
Загрузите из внешнего файла модель структуры кубического кластера никеля Ni₁₇₂ (File → Load structure…). В диалоговом окне открытия файла найдите директорию Structures и в ней — файл Ni172_cube.hin. Откройте.
Вызовите команду Graph… из меню View. Задайте радиус обрезки, заведомо превышающий расстояние между наиболее удаленными атомами в структуре, например, 1000000 a₀. Для этого в поле Maximum введите 1000000, затем введите 1000000 в поле Exact value и обязательно нажмите Enter для применения изменений. При этом в главном окне должен отрисоваться полный граф наноструктуры. Закройте окно Graph нажатием кнопки OK.
Для фиксирования графа вызовите команду Lock graph из меню Edit и в ответ на запрос о подтверждении нажмите Yes.
Смените способ представления структуры с графового на шаровое. Для этого из меню View вызовите команду Performance… и в появившемся одноименном окне установите переключатель в группе View в положение Spheres. Ползунком Sphere radius задайте желаемый радиус атомов-сфер.
В диалоговом окне Settings (Edit → Set parameters…) укажите (либо с помощью кнопки Load parameters… загрузите из файла Potential_params.txt) параметры потенциалов, как показано на рис. 1.
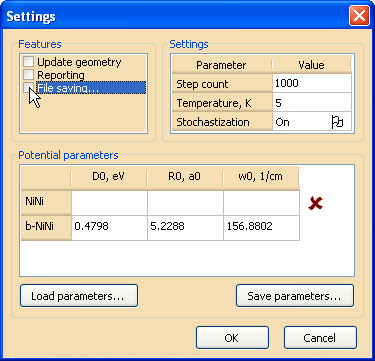
Рис. 1. Диалоговое окно выставления опций и параметров потенциалов
Установите параметры в группе Settings, как показано на рис. 1. Не закрывайте пока окно Settings. Установите флажок File saving… в группе Features. При попытке установки флажка вам будет предложено указать путь и имя log-файла, в который будут заноситься данные расчета на каждой итерации вычислительной процедуры. Задайте понятное имя файла (например, Ni172_5K.log) и нажмите кнопку Сохранить.
Осуществите один проход вычислительной процедуры, вызвав команду Evolve из меню Edit. Если этого окажется недостаточно для достижения ближней окрестности точки стационарного аттрактора (см. рис. 2), выполните расчет повторно.
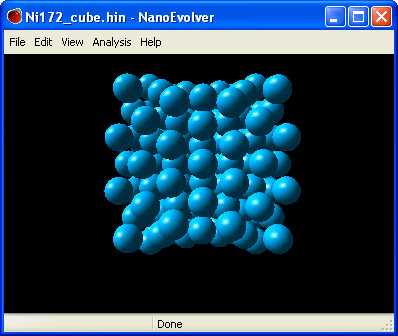
Рис. 2. Вид стационарного неравновесного аттрактора при T = 5 K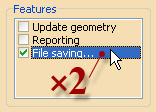
Рис. 3. Открытие log-файла из окна Set parameters
Вновь откройте окно Settings (Edit → Set parameters…). Выполните двойной щелчок мышью по надписи File saving… (не по флажку, а именно по надписи), либо нажмите Ctrl+Enter, установив фокус на данный пункт группы Features. Это действие должно привести к открытию сохраненного на диске log-файла в табличном процессоре Microsoft® Excel. (Если по каким-либо причинам при двойном клике отчет не открывается, запустите MS Excel вручную и откройте log-файл средствами самого Excel.) В случае, если на вашем компьютере не установлен Microsoft Office, воспользуйтесь иным табличным процессором, аналогичным MS Excel, например, OpenOffice.org Calc, полностью скопировав в него содержимое log-файла. Общая последовательность действий в любом случае в целом неизменна.
Просмотрите log-файл в окне табличного процессора MS Excel (или OpenOffice.org Calc). Поясним значение столбцов таблицы log-файла.
1. Step, nm — длина единичной трансляции изображающей точки в пространстве конфигураций наносистемы на каждой итерации вычислительной процедуры (нм);
2. E, kJ/mole — полная энергия связи наносистемы на каждой итерации вычислительной процедуры (кДж/моль);
3. ||grad E||, N — норма градиента полной энергии связи в текущем положении изображающей точки на поверхности потенциальной энергии (Н);
4. dt, s — квант времени жизни запутанного состояния квазиэлектронной системы (с);
5. RootSumSqr и SumSqr — технические данные;
Задание. Используя стандартные возможности табличного процессора MS Excel (или OpenOffice.org Calc) постройте развертки эволюции нанокластера Ni₁₇₂ в координатах
1. энергия (E, кДж/моль) — время эволюции (t, пс)
2. энергия (E, кДж/моль) — путь изображающей точки (S, нм)
3. квант времени (Δt, фс) — время эволюции (t, пс)
Примечание 1. Указанные па́ры вида «A — B» означают, что при построении разверток первая из величин (A) должна быть зависимой переменной и откладываться по оси ординат, а вторая (B) — независимым аргументом, который следует откладывать по оси абсцисс.
Примечание 2. Обратите внимание на требуемые в задаче единицы измерения каждой из величин.
Примечание 3. Общее время эволюции, прошедшее к моменту i-й итерации определите суммированием кванта времени Δt_i на i-й итерации и общего времени на (i − 1)-й итерации. Аналогично — для общего пути, пройденного изображающей точкой.
Если вы чувствуете себя уверенно при работе в среде MS Excel, можете приступать к выполнению задания. В противном случае вы можете «вооружиться» пошаговой инструкцией.
Инструкция
1. Для начала удалите неиспользуемые в задаче столбцы C, E и F, чтобы они не загромождали рабочее пространство листа. Для этого выделите столбцы полностью и выберите команду Удалить из контекстного меню.
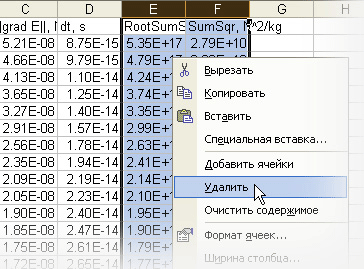
  Рис. i. Удаление неиспользуемых столбцов
2. Для удобства дальнейшей работы можно (условно) зарезервировать имеющиеся справа свободные столбцы под данные, которые будут использоваться при непосредственном построении разверток. Можно, например, использовать различные цвета заливки ячеек, впрочем, это необязательно. Подпишите столбцы для будущих данных построения.
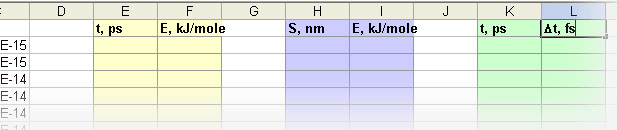
  Рис. ii. «Зарезервированные» для данных столбцы
  Чтобы не путаться, желательно выбрать те же столбцы, что показаны на рис. ii, поскольку в дальнейшем изложении будет использоваться соответствующая адресация ячеек.
3. В столбце B выделите все числовые данные, которые идут вниз, начиная от ячейки B2 и до последней непустой ячейки. Скопируйте данные (Ctrl+C). Заполните скопированными в буфер обмена данными столбцы F и I.
  Рис. iii. Перенос данных полной энергии связи
4. Для расчета прошедшего к моменту каждой итерации общего времени эволюции (столбцы E и K) следуйте такой схеме. Поскольку отсчет времени ведется от начала эволюции, то очевидно, что начальное значение t равно нулю. Введите 0 в ячейку E2. В соответствии с примечанием 3 выше введите в ячейку E3 следующую формулу:
  =E2+C2*1E+12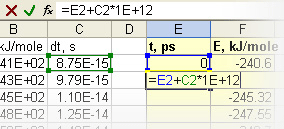
  Рис. iv. Ввод формулы в ячейку для расчета общего времени эволюции
  Мы одновременно произвели пересчет из секунд в пикосекунды, как требовалось в задании.
5. Не снимая выделение с ячейки E3, дважды щелкните по черному квадратику в правом нижнем углу рамки, обрамляющей ячейку. При этом должно произойти распространение формулы на все нижележащие ячейки.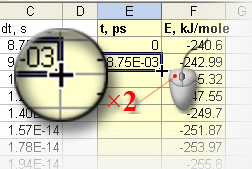
  Рис. v. Распространение формулы на нижележащие ячейки
6. Выделите числа в столбце E, скопируйте выделение в буфер обмена. Щелкните правой кнопкой мыши по ячейке K2 и из появившегося контекстного меню выберите пункт Специальная вставка….
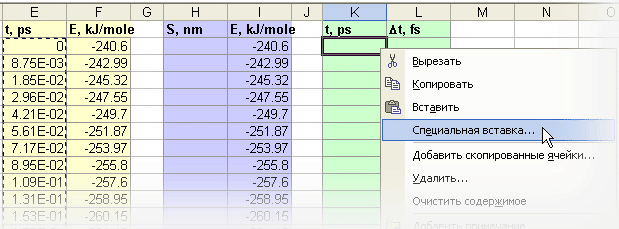
  Рис. vi. Вызов окна Специальная вставка
  В окне Специальная вставка установите переключатель в положение Значения и нажмите кнопку OK.
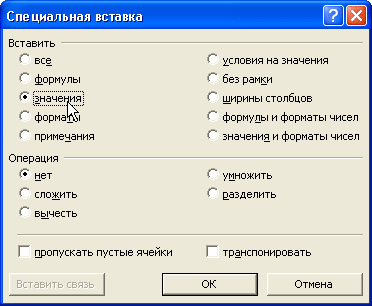
  Рис. vii. Окно Специальная вставка. Настройки для вставки только значений в ячейках
7. Используя аналогичную схему, заполните столбец H значениями пройденного изображающей точкой полного пути на момент каждой итерации. А именно, как и прежде введите значение 0 в ячейку H2 (отсчет пройденного пути — от начала эволюции). В ячейку H3 введите формулу
  =H2+A2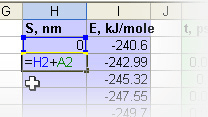
  Рис. viii. Ввод формулы в ячейку для расчета длины пути изображающей точки
  Не убирая фокуса с ячейки H2, дважды щелкните по кадратику в правом нижнем углу рамки ячейки, чтобы заполнить нижележащие ячейки.
8. Наконец, заполните значениями столбец L. Для этого введите в ячейку L2 формулу
  =C2*1E+15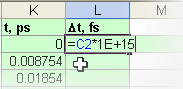
  Рис. ix. Ввод формулы в ячейку для пересчета кванта времени в фемтосекундах
  Распространите формулу на нижележащие ячейки.
9. Выделите полностью все численные данные в столбцах E и F и вызовите окно «Мастера диаграмм» (меню Вставка, команда Диаграмма…).
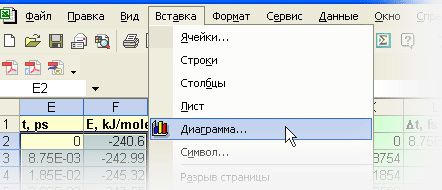
  Рис. x. Команда вставки диаграммы
10. На первом шаге Мастера выберите тип диаграммы «Точечная» и вид сглаженной линии без маркеров.
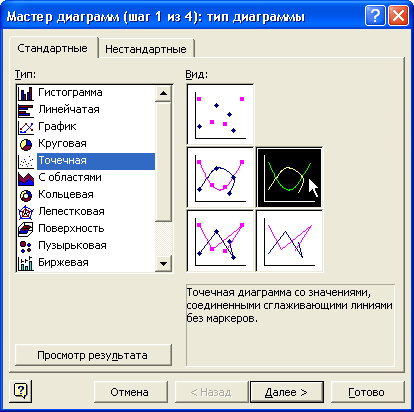
  Рис. xi. Первый шаг «Мастера диаграмм»
Пример оформленного до конца задания показан на рис. 4.
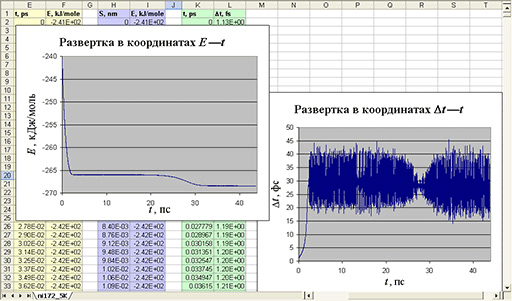
Рис. 4. Окончательный вид рабочего листа Excel. Случай криогенных температур
Проанализируйте вид полученных разверток. Сделайте выводы относительно общего характера поведения полной энергии связи E и кванта времени Δt на протяжении эволюционного процесса, а также относительно более тонких деталей и подробностей хода разверток. Отметьте суммарную длительность процесса достижения стационарного неравновесного аттрактора. Эта величина важна в частности в том отношении, что существуют экспериментальные спектроскопические методы регистрации времени полной трансформации наночастиц.
Мысленно разделите график изменения полной энергии связи во времени на более или менее однородные участки и соотнесите эти участки с событиями, имевшими место в эволюции наносистемы. Чему отвечают переходные области между этими однородными участками? Обратите внимание на масштаб флуктуаций энергии около стационарного значения при выбранной для расчетов криогенной температуре.
Примерно в том же духе выполните анализ временно́й развертки кванта времени Δt. Оцените визуально, а затем рассчитайте при помощи функций MS Excel (или OpenOffice.org Calc) среднее значение величины Δt на протяжении эволюции. (Для расчета среднего значения массива численных данных в MS Excel можно использовать функцию СРЗНАЧ, а в OpenOffice.org Calc — функцию AVERAGE.) Также обратите внимание на размах девиаций относительно среднего.
Сохраните рабочую книгу Excel в формате *.xls для последующего дополнительного рассмотрения.
Повторите построения для случая температуры, близкой к комнатной (например, T = 300 K). Пример оформленных результатов расчетов при T = 300 K показан на рис. 5.
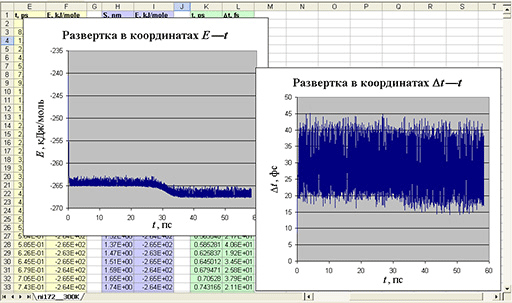
Рис. 5. Окончательный вид рабочего листа Excel. Случай комнатных температур
Сравните результаты расчетов для двух температур. Оцените масштабы флуктуаций величин. Сделайте вывод о характере влияния температуры на общий вид разверток эволюции нанотрансформеров, а следовательно, на характер их фемтосекундной корпоративной динамики.

Вопросы для контроля

Многие из приведенных ниже вопросов были обозначены в материалах лекций и по ходу выполнения лабораторной работы. Суммируем и расширим их здесь.

Укажите характерные временны́е масштабы квантовых процессов наномира. Приведите по примеру для каждого временно́го масштаба.
Укажите на известные вам достижения экспериментальной и/или теоретической науки в области фемтосекундной динамики на наноуровне.
Опишите вкратце сущность механизма временно́й дискретизации процессов эволюции мультиструктурных частиц.
Назовите основные, на ваш взгляд, признаки мультичастиц-трансформеров и их отличия от «обычных» наночастиц.
Какие фундаментальные процессы наномира «вершат» эволюцию мультичастиц, их динамику и кинематику?
Какие, по-вашему, предпосылки существуют для феномена самоорганизации на наноуровне?
Какие из известных вам и наиболее распространенных методов моделирования динамики наносистем не могут использоваться при решении задачи описания корпоративной эволюции неравновесных наночастиц и почему?
В чем суть модели стохастической фемтосекундной корпоративной динамики наносистем?

Литература

Beznosjuk S.A., Minaev B.F., Dajanov R.D., Muldachmetov Z.M. Approximating quasiparticle density functional calculations of small active clusters: strong electron correlation effects // Int. J. Quant. Chem. 1990. 38(6). 779–797.
Beznosjuk S.A., Minaev B.F., Muldachmetov Z.M. Informative energetic structure and electronic multistability of condensed state // J. Mol. Struct. (Theochem). 1991. 224. 125–127.
Безносюк С.А., Потекаев А.И., Жуковский М.С., Жуковская Т.М., Фомина Л.В. Многоуровневое строение, физико-химические и информационные свойства вещества. Томск: НТЛ, 2005. 264 с.
Безносюк С.А., Важенин С.В. Особенности влияния упаковок атомов на фемтосекундные корпоративные трансформации металлических наночастиц // Материалы Открытой школы-конференции стран СНГ «Ультрамелкозернистые и наноструктурные материалы-2008», Перспективные материалы, Специальный выпуск (7). 2009. 39–44.
Важенин С.В., Безносюк С.А., Жуковский М.С., Жуковская Т.М. Корпоративная эволюция наночастиц в условиях сильной неравновесности конденсированных состояний // Фундаментальные проблемы современного материаловедения. 2008. 4. 7–13.
Zurek W.H. Reduction of the Wave Packet: How Long Does It Take? // NATO ASI “Frontiers of Nonequilibrium Statistical Physics” Edited by G.T. Moore and M.O. Scully. New York: Plenum, 1986. Vol. B135, pp. 145–149.