Исследование самоорганизации наноструктур графена с помощью модуля «Молекулярная наномеханика»
Обоснование и проблематика
В развивающихся примерно с середины XX в. феноменологических теориях гибких мембран было показано в гармоническом приближении, что возможность существования двумерных структур, таких как мембраны, сильно ограничена из-за наличия термических флуктуаций, которые приводят к тому, что атомные смещения в направлении, нормальном к плоскости, логарифмически расходятся с ростом размеров образца. Учет нелинейных членов в тензоре деформации, тем не менее, позволял в некотором отношении обосновать возможность существования двумерных в целом структур за счет ангармонического взаимодействия продольных и изгибных мод, однако по-прежнему предсказывал неизбежность заметного «смятия» двумерных образований.
Открытие в 2004 г. первого двумерного кристалла — графена [1] — позволило сделать значительный шаг в обосновании возможности существования структур в двух измерениях. Отсутствие в образцах графена существенных дефектов типа дислокаций, его эластичность и другие механические свойства позволили считать его действительно двумерным кристаллом. Тем не менее, исследования свободно взвешенных образцов с помощью просвечивающей электронной микроскопии [2, 3] и изучение образцов, нанесенных на подложку диоксида кремния, методом сканирующей туннельной микроскопии [4] показали, что графен не является идеально плоским, но присутствуют волнообразные деформации, выводящие монослой в третье измерение.
В настоящее время существует несколько принятых обоснований наличия таких деформаций. Но по существу они в большинстве своем следуют из модельных построений и с переменным успехом воспроизводят экспериментальные наблюдения. До тех пор пока не разработана новая теория двумерных мембран, которая учитывала бы современное состояние вопроса (в частности, по графену), моделирование остается неотъемлемой составляющей большинства научных работ — как теоретического, так и экспериментального содержания.
Целью работы является выяснение особенностей структуры наночастиц графена как результата неравновесного процесса самоорганизации монослоя в определенном температурном режиме эволюции. В качестве одной из задач выступает проверка применимости модели диссипативной эволюции наносистем [5] к описанию структурной организации монослоя графена наноскопических размеров в различных температурных режимах.
Порядок выполнения работы
Запустите программу «NanoEvolver» — Dissipative (версия 4.2), если она еще не запущена.
При необходимости ознакомьтесь с руководством по основам работы с программой. Для этого вызовите команду Index из меню Help, или же нажмите клавишу F1. Вы можете всякий раз обращаться к руководству при возникновении затруднений.
Загрузите из внешнего файла модель структуры графена. Загрузка осуществляется посредством команды Load structure… из меню File. В диалоговом окне открытия файла найдите директорию Structures и в ней — файл Graphene.nev. Если файл не отображается, смените тип отображаемых файлов, используя выпадающий список в нижней части диалогового окна.
Рис. 1. Смена типа отображаемых файлов Расположите модель на экране так, чтобы обеспечить удобство ее обзора. Используйте клавиши ←↑↓→ для вращения модели в пространстве; Insert/Delete — для приближения/отдаления; Page Up/Page Down — для перемещения по вертикали; Home/End — для перемещения по горизонтали.

Рис. 2. Вид модели графенового монослоя в окне «NanoEvolver» В «NanoEvolver» используются аппроксимирующие парные потенциалы в форме функции Морзе. Параметры потенциалов — D0 (энергия диссоциации), R0 (равновесное расстояние) и ω (частота колебаний) — чаще всего рассчитываются неэмпирическими методами ab initio, а подходящая аналитическая форма электронным термам придается с использованием метода аппроксимации по дискретным расчетным точкам. В данном случае расчеты параметров потенциала связи C—C в графене выполнены методом нелокального функционала плотности в пакете программ «Winbond».
Задание параметров межатомных потенциалов для загруженной модели и определение установок расчетной процедуры.
Указание параметров потенциалов, а также некоторых важных опций и параметров, влияющих на ход расчетной процедуры, производится в диалоговом окне Settings (см. рис. 3), вызвать которое можно с помощью команды Set parameters… меню Edit.
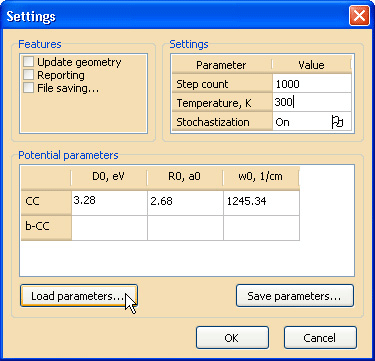
Рис. 3. Диалоговое окно выставления опций и параметров Установите параметры, как показано на рис. 3. Параметры межатомных потенциалов введите либо вручную, либо, нажав на кнопку Load parameters…, загрузите эти данные из внешнего файла параметров Potential_params.txt, который расположен в той же папке, что и загруженная структура. Подробные сведения обо всех используемых здесь опциях и флагах вы можете найти в руководстве к программе «NanoEvolver» (см. главы «Задание параметров межатомных потенциалов» и «Задание параметров оптимизации»). Установите флажок File saving… в группе Features и задайте имя log-файла в появившемся диалоговом окне сохранения.
Сохраните отчет во внешнем файле. Для этого вызовите команду Save report as… из меню File. Укажите путь и разумное имя файла (например, GrapheneInit300K.htm), нажмите Сохранить. «NanoEvolver» сохраняет отчеты в удобном формате гипертекста, можете сейчас просмотреть сохраненный на диске отчет, используя любой установленный на компьютере браузер. Анализируя отчет, обратите внимание на единицы измерения и порядок величин. Не закрывайте пока открытый отчет.
Вернитесь к окну «NanoEvolver». Выполните оценку ближнего порядка в начальной идеальной структуре графена. Оценить ближний порядок позволяет парная корреляционная функция, или радиальная функция распределения g(R). Средства расчета и построения функции g(R) доступны при вызове команды Radial distribution function… из меню Analysis (см. рис. 4).
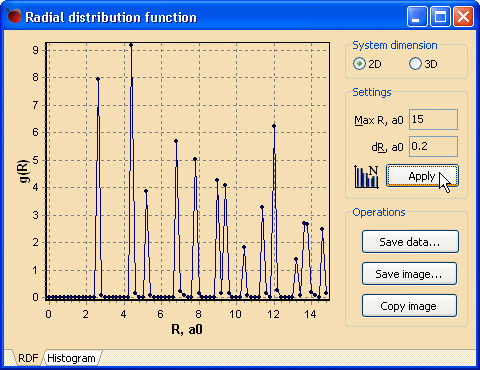
Рис. 4. Радиальная функция распределения «идеального» планарного графенового монослоя Изначальные настройки окна Radial distribution function требуют корректировки в случае графена. Все опции доступны для изменения на панели справа от графика.
- Установите переключатель в положение 2D. Расчет функции g(R) отличен для объемных и, скажем, поверхностных структур в силу вхождения в выражение для g(R) макроскопической плотности: измеряется соответственно плотность в объеме (ρ) или в слое (σ).
- Установите в поле Max R желаемое расстояние, то есть диапазон, в котором будет построен график радиальной функции расперделения. От этого будет зависеть, сколько координационных сфер будет захвачено при построении.
- Задайте в поле ввода dR шаг между точами при расчете функции. Учитывая равновесную длину связи C—C в графене (2.68 a0), интервал в 0.2 a0 является вполне достаточным, как показано на рис. 4.
- Нажмите кнопку Apply для применения измененных настроек и пересчета графика. При необходимости можете поэкспериментировать с настройками для получения максимально отчетливого представления графика. Оцените остроту пиков, сделайте вывод о степени разброса длин связей и степени регулярности идеальной начальной структуры.
Нажатием на кнопку Save image… сохраните графическое изображение для последующего сравнительного анализа.
Закройте окно Radial distribution function и приступайте к следующему — основному — этапу лабораторной работы. Раскройте меню Edit главного окна программы «NanoEvolver» и выберите пункт Evolve. В зависимости от количества итераций, выставленного в окне Settings, а также от размеров выбранного для расчетов образца, процедура моделирования процесса самоорганизации может занять несколько минут, поэтому вы можете временно переключиться на работу с уже имеющимися данными в открытых окнах вне программы «NanoEvolver». За время, пока идут расчеты, повторно просмотрите отчет по начальной структуре; выполните перевод значений характеристик в единицы СИ, используя либо карманный калькулятор, либо «Калькулятор» Windows. При возможности проведите сравнение энергии когезии в расчете на связь для имеющейся начальной структуры графена и энергий когезии в наноалмазе (237.4 кДж/моль), нанокарбине (380.2 кДж/моль).

Рис. 5. Окно с кратким отчетом при завершении расчетной процедуры По завершении первого «прогона» процедуры отметьте (запомните или запишите) текущие значения полной энергии связи и градиента энергии. В окне Settings установите меньшее число итераций (например, 500) и прогоните дополнительный расчет. Если в результате повторных расчетов значения энергии и градиента меняются мало, можно переходить к следующему шагу.
Оцените визуально изменения, которые произошли в геометрии монослоя. Для получения наиболее отчетливой картины деформаций поверхности вы можете вращать и перемещать модель в пространстве, а также подобрать другие цвета для атомов структуры и для фона. Подбор цвета атомов и фона осуществляется посредством команд Define atoms color… и Define window color… соответственно.

Рис. 6. Геометрия графенового монослоя при температуре T = 300 K как результат расчетов в программе «NanoEvolver» Сохраните отчет (File → Save report as…) для полученной в результате структуры (назовите файл, например, GrapheneFin300K.htm). Исследуйте отчет. Обратите внимание на изменение полной энергии связи, если таковое имеется, пересчитайте характеристики в единицы СИ. Согласуется ли наличие «шероховатости» поверхности графена со значением энергии изгибных деформаций для конечной структуры?
Постройте график радиальной функции распределения для конечной структуры (Analysis → Radial distribution function…). Имеются ли изменения в строении ближнего порядка по сравнению с идеально плоским монослоем? Если да, в чем это выражается? (Если вы сохраняли изображение на шаге 7, можете открыть его для сравнения.)
Вызав команду Height distribution… из меню Analysis, вы можете запустить утилиту «hPlot» для построения диаграммы распределения высот нормальных отклонений Δz атомов в монослое графена (см. рис. 7). Можно ли сказать, что полученное вами распределение атомных смещений от базовой плоскости удовлетворительно описывается гауссовой кривой? Обратите внимание на диапазон варьирования высот, то есть максимальную амплитуду внеплоскостных деформаций поверхности. Данная величина измерена и в ряде экспериментов методами просвечивающей электронной микроскопии [2, 3], сканирующей электронной микроскопии [4] и т.д., то есть позволяет верифицировать расчетные модели сравнением с экспериментом.
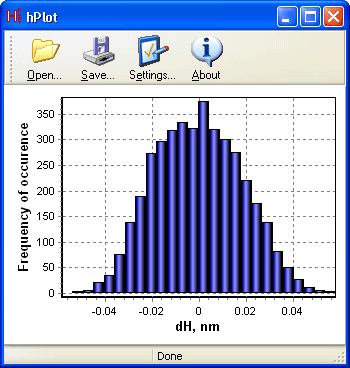
Рис. 7. Распределение высот нормальных отклонений Δz атомов в монослое графена Сохраните на диск модель конечной структуры как результат своих расчетов. Вызовите для этого команду Save structure… из меню File. В диалоговом окне сохранения укажите тип файлов NE files (*.nev).
Рис. 8. Выбор формата сохранения структуры При необходимости можно сохранить для отчета графическое изображение модели, как она видна в окне программы «NanoEvolver». Команда сохранения Save image as… находится в пункте File главного меню программы.
Откройте log-файл в табличном процессоре Microsoft® Excel (Сто́ит напомнить, что это действие быстро выполняется при даойном щелчке на пункте File saving… в окне Set parameters). Постройте развертки полной энергии связи и кванта времени в зависимости от времени эволюции. Сопоставьте средние значения Δt для графена с одной стороны и для металлических систем — с другой стороны. Построение эволюционных разверток металлических кластеров было выполнено вами в лабораторной работе «Исследование фемтосекундной корпоративной динамики неравновесных наносистем» (см. также инструкции).
Вопросы для контроля
Многие из приведенных ниже вопросов были обозначены в материалах лекций и по ходу выполнения лабораторной работы. Суммируем и расширим их здесь.
- Как согласуются классическая теория и эксперимент в вопросе о стабильности систем в двух измерениях?
- С именами каких ученых вы ассоциируете современное состояние проблемы графена?
- Как выявляется факт присутствия неоднородностей поверхности графена в эксперименте, и какие теоретические/модельные обоснования приводятся для наблюдаемых феноменов?
- Какого рода модельные подходы наиболее широко применяются к решению задачи описания структурных особенностей графена? Имеются ли какие-либо преимущества одних перед другими?
- Какие вам известны подходы для моделирования неравновесной самоорганизации наночастиц? Какие используются в задачах с графеном?
- Как вы думаете, может ли графен быть использован в качестве мембраны с широким диапазоном термической устойчивости?
- Используя результаты проведенных вами расчетов, могли бы вы сказать, насколько сильно влияние термических флуктуаций изменяет структуру графена в условиях комнатной температуры?
- Как бы вы оценили модель корпоративной стохастической эволюции наночастиц в приложении к задаче описания структуры графеновой поверхности?
Литература
- Novoselov K.S., Jiang D., Schedin F., Booth T.J., Khotkevich V.V., Morozov S.V., Geim A.K. Two-dimensional atomic crystals // Proc. Natl. Acad. Sci. USA. 2005. 102, 10451—10453.
- Meyer J.C., Geim A.K., Katsnelson M.I., Novoselov K.S., Obergfell D., Roth S., Girit Ç, Zettl A. On the roughness of single- and bi-layer graphene membranes // Solid State Communications. 2007. 143(1—2). 101—109.
- Meyer J.C., Geim A.K., Katsnelson M.I., Novoselov K.S., Booth T.J., Roth S. The structure of suspended graphene sheets // Nature. 2007. 446. 60—63.
- Stolyarova E., Rim K.T., Ryu S., Maultzsch J., Kim P., Brus L.E., Heinz T.F., Hybertzen M.S., Flynn G.W. High-resolution scanning tunneling microscopy imaging of mesoscopic graphene sheets on an insulating surface // Proc. Nat. Ac. Sci. (USA) 2007. 104. 9209—9212.
- Безносюк С.А., Важенин С.В., Жуковский М.С., Жуковская Т.М., Маслова О.А. Законы и закономерности движения частиц в наномире // Фундаментальные проблемы современного материаловедения. 2007. 4. 35—41.

