Компьютерное моделирование самосборки и самоорганизации наносистем с использованием метода Монте-Карло

Интенсивные исследования в области нанотехнологий, активизировавшиеся на рубеже XX—XXI веков, становятся двигателем происходящих в настоящее время кардинальных изменений в промышленном производстве и ведут к качественному скачку в развитии методов и средств обработки информации, синтеза новых материалов, разработке новых научных подходов к познанию материи.

В настоящее время нанотехнология находится в самом начале пути, и лишь отдельные простейшие наноструктуры могут создаваться контролируемым образом. Наука об атомах и простых молекулах, с одной стороны, и наука о веществе, охватывающая микроструктуры и более крупные масштабы, с другой стороны, в целом, вполне сформированы. Остается область нанометрового масштаба, которая определяет фундаментальные свойства материалов и позволяет управлять ими.

Наноструктуры с течением времени начинают играть все большую роль в молекулярной биологии, химии, материаловедении и физике твердого тела. Модификация свойств известных материалов с использованием частиц малого размера и разработка процессов формирования наночастиц являются предметом изучения современного материаловедения.

Здесь ясно прослеживается одна тенденция: нанотехнология делает конструирование наиболее важной частью любого разрабатываемого процесса. Объем конструкторской работы неизмеримо возрастает ввиду ее сложности. Невероятно важным при этом становится планирование далеко идущих изменений, поэтому все большую важность начинают играть методы компьютерного моделирования и расчета.

Методы изучения многочастичных наносистем

Если попытаться обозначить основные численные методы для многочастичных систем, то они сводятся к следующим четырем: квантово-теоретические расчеты из первых принципов (ab initio), молекулярная механика, метод Монте-Карло и метод молекулярной динамики.

Поскольку решить уравнение Шредингера для системы многих частиц невозможно (при увеличении числа частиц необходимое время расчета растет экспоненциально), квантово-теоретический подход состоит в нахождении приближений и возможностей разделения переменных, позволяющих упростить схему вычислений. Из наиболее распространенных методов расчета из первых принципов можно назвать методы самосогласованного поля, линейной комбинации атомных орбиталей и функционала плотности.

В отличие от методов расчета из первых принципов, методы молекулярной механики и молекулярной динамики основаны на классической механике. Частицы рассматриваются как материальные точки, взаимодействующие через силовые поля, которые, в свою очередь, определяются потенциалами взаимодействия. Целью молекулярной механики (как и расчетов из первых принципов) является нахождение устойчивых конфигураций для систем многих частиц, т. е. определение седловых точек (локальных минимумов) на поверхности потенциальной энергии.

Управление процессами самоорганизации вещества

Важной чертой нанотехнологии является возможность управления процессами самоорганизации вещества. Примером такого управления могут служить магнитные жидкости — феррофлюиды, которые уже сейчас находят применение в самых различных областях современного производства. Феррофлюид представляет собой жидкость, содержащую очень маленькие ферромагнитные частички. Это, как правило, частички магнетита размером около 10 нанометров. Засчет этого жидкость в очень большой мере подвержена влиянию магнитных полей и демонстрирует причудливое "поведение" внутри магнитного поля.

Также повышенный интерес в настоящее время вызывают исследования нанокластеров металлов. Это обусловлено тем, что изучаемые системы являются перспективными материалами для применения в широком спектре отраслей современной индустрии: полупроводниковой технике, наноэлектронике, нанометрологии, катализе, фотокатализе, биологии и медицине. Множество работ направлено на поиск новых перспективных технологий контролируемого получения частиц, характеризующихся однородной дисперсностью и составом. В свою очередь, становится важным теоретическое исследование и предсказание свойств таких материалов (о чем свидетельствует множество работ опубликованных в этой области за последнее время) для достижения большей эффективности производства и сокращения сроков коммерциализации готовых продуктов. Получение новых знаний о кинетике процессов формирования нанокластеров металлов открывает возможность целенаправленного конструирования новых материалов с заранее заданными свойствами.

В последнее десятилетие большой интерес вызывают металлические нанокластеры, которые представляют собой почти монодисперсные металлические частицы, имеющие диаметр менее 10 нм. Нанокластеры имеют уникальные свойства, связанные с их промежуточным положением между объемной фазой и индивидуальными атомными или молекулярными частицами.

Эти вещества имеют большие перспективы в качестве новых типов высокоактивных и селективных катализаторов. Наноразмерный катализ приводит как к возрастанию активности катализатора и его селективности, так и к регулированию процессов химической реакции и свойств конечного продукта. Такая возможность проявляется не только путем изменения размеров нанокластеров, входящих в катализатор, и удельной поверхности, но и за счет появления новых размерных свойств и химического состава поверхности.

Наличие уникальных электронных и магнитных свойств делает металлические нанокластеры перспективным материалом для создания квантовых вычислительных устройств. В таких компьютерах квантовые эффекты, например, магнитного квантового туннелирования или гигантского магнитного резонанса не ограничивают, а расширяют возможности вычислений и увеличивают быстродействие.

Цель лекции

Цель лекции: Знакомство с методами решения задач по проектированию самосборки и самоорганизации нанокластеров.

Методы получения металлических нанокластеров

Существует четыре основных набора методов синтеза металлических нанокластеров:

1. Методы испарения (конденсации);
2. Методы осаждения из коллоидных растворов;
3. Методы термического разложения и восстановления;
4. Механические методы получения.

Свойства металлических нанокластеров

Основные характеристики кластеров связаны с энергией ионизации кластеров, энергией сродства к электрону, шириной энергетической щели между зонообразующими уровнями. Кроме того, здесь появляются магнитные характеристики, обусловленные d-оболочкой атомов кластеров.

Структурные особенности

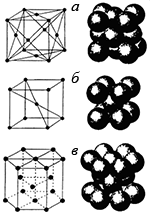
Обычно кристаллическая структура наночастицы такая же, как и у объемного материала, но с несколько отличающимся параметром решетки. Однако в некоторых случаях малые частицы с размерами менее 5 нм могут иметь другую структуру. Например, показано, что частицы золота с размерами 3–5 нм имеют икосаэдрическую структуру, хотя в объеме золото кристаллизуется в ГЦК-решетку. У очень маленьких наночастиц все или почти все атомы находятся на поверхности. Колебания поверхностных атомов ограничены соседями слабее, чем колебания внутренних, так что они могут сильнее отклоняться от своих равновесных положений. Это приводит к изменениям в структуре частицы. Так, при повышении температуры флуктуации могут привести к исчезновению порядка и формированию агрегата атомов, похожего на каплю жидкости.

Рассмотрим алюминиевый кластер. На основе критерия максимизации количества связей при минимизации объема, а также того факта, что в объеме структурой алюминия является ГЦК, можно ожидать, что структура такой наночастицы также будет ГЦК. Однако вычисления молекулярных орбиталей по методу функционалов плотности предсказывают, что наименьшую энергию имеет икосаэдрическая форма, то есть, вероятно, изменение структуры. Пока не существует экспериментальных данных о структуре алюминиевых наночастиц, подтверждающих такое предположение. Экспериментальное определение структуры малых металлических наночастиц весьма сложно, так что количество таких данных невелико. Для кластеров менее 8 нм в диаметре наблюдались отклонения от ГЦК-структуры.

Следует отметить, что структура изолированной наночастицы может отличаться от лиганд-стабилизированной структуры. Лиганд-стабилизацией называется присоединение неметаллических ионных групп к металлическим атомам или ионам. Изменение структуры может отразиться на многих свойтвах, в частности — на электронной структуре.

Электронные свойства

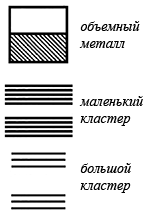
Когда атомы формируют решетку, их дискретные энергетические уровни расщепляются в энергетические зоны. Термин плотность состояний означает количество энергетических уровней в заданном интервале энергий. В металле верхняя энергетическая зона заполнена не до конца. В случае полупроводника верхняя занятая зона, называемая валентной, заполнена до конца и отделяется от следующей, пустой зоны небольшим промежутком, называемым энергетической щелью. Когда частица металла уменьшается в размерах до нескольких сотен атомов, плотность состояний в зоне проводимости — верхней зоне, содержащей электроны — радикально меняется. Непрерывная плотность состояний в зоне заменяется набором дискретных уровней, интервалы между которыми могут оказаться больше, чем тепловая энергия k_BT, что приводит к образованию щели. Изменения электронной структуры при переходе от объемного кристалла к большому кластеру, а затем к маленькому кластеру с размерами меньше 15 атомов, показаны рисунке.

Маленький кластер аналогичен молекуле с ее дискретным набором энергетических уровней, связывающими и антисвязывающими орбиталями. В конце концов, можно уменьшить кластер до размеров, при которых расстояние между противоположными гранями приблизится к длине волны электрона. В таком случае энергетические уровни могут быть получены путем рассмотрения квантовой задачи о частице в потенциальном ящике. Это называется квантовым размерным эффектом.

Кластеры переходных металлов сложную электронную структуру, поскольку у них имеются электронные d- и f-оболочки. Стабильность и реакционная способность кластеров обусловливается двумя рядами магических чисел, один из которых связан с электронной оболочкой, другой — с геометрическим фактором (плотнейшей упаковкой). Свойства кластеров переходных металлов, включая Cu, Ag и Au, определяются как электронной, так и геометрической структурой. Кроме того, для кластеров переходных металлов особое значение приобретает способность атомов находится в разных окислительных состояниях.

Изменение энергии ионизации кластеров с различным размером представляет собой весьма эффективный подход для изучения эволюции свойств кластеров к свойствам массивного материала и дает прямой выход на их реакционную способность, поскольку определяет способность к переносу электронов в химических реакциях.

Экспериментальные данные для кластеров кластеров Fe_n и Со_n при n = 1 – 100 свидетельствует о значительных изменениях энергии ионизации в области малых кластеров. Эти колебания уменьшаются с ростом кластеров и при n более 25 зависимость практически отсутствует. Столь значительные отклонения могут быть следствием либо отличия структуры кластера от массивного материала, либо, что более вероятно, являются следствием сильного влияния электронной структуры кластера, которая подвержена перестройке при заполнении d-оболочки. В пользу такого объяснения служит тот факт, что величины Е, для кластеров с четным числом атомов больше, чем с нечетным числом. Эти колебания свидетельствуют о формировании d-оболочки.

Сродство к электрону определяется как уменьшение электронной энергии кластера при добавлении к нему одного электрона.

Для кластеров с числом атомов 7 – 16 наблюдается изменение энергии при четном и нечетном числе атомов в кластере, что связывается со степенью электронной локализации и вырождения. Кластеры с четным числом атомов обладают замкнутой электронной оболочкой. Добавочный электрон в отрицательном кластерном ионе занимает нижнюю незанятую молекулярную орбиталь, что и приводит к понижению энергии сродства к электрону, Исследование таких кластеров дает возможность определить энергетическую щель между низшей занятой молекулярной орбиталью и высшей незанятой молекулярной орбиталью. Особенно значительны скачки в уменьшении энергии сродства к электрону и в увеличении энергетической щели для кластеров с числом атомов 8, 10 и 16. Эти особенности построения электронной оболочки кластера находятся в хорошей корреляции с его химической активностью при взаимодейвии с молекулярным водородом, Кластеры с максимальной величиной энергетической щели обладают самой низкой реакционной способностью. Этот факт может иметь практическое значение для материалов водородной энергетики.

Для кластеров с числом атомов 17 – 25 энергия сродства к электрону плавно возрастает, и нет уже колебаний на четные и нечетные числа атомов в кластере. Энергетическая щель между нижними заполненными и верхними незаполненными орбиталями близка к нулю и убывает с ростом числа атомов в кластере. Можно ожидать, что большие кластеры будут иметь высокую реакционную способность, подобно массивному металлу.

Оптические свойства

Цвет материала определяется длиной световых волн, которые он поглощает. Поглощение происходит вследствие возбуждения электронов фотонами падающего света с нижних, заполненных энертетических уровней материала на незаполненные верхние. Кластеры разных размеров имеют разную электронную структуру и, соответственно, разные расстояния между уровнями. Это означает, что кластеры разных размеров могут отличаться по цвету, и размер кластера можно использовать при проектировании цвета материалов.

Магнитные свойства

На энергетических уровнях, занятых четным количеством электронов, магнитные моменты последних попарно противоположны, так что полный момент атома равен нулю. Таким образом, большинство атомов в твердых телах не имеют магнитного момента, однако существуют ионы переходных элементов, таких как железо, марганец и кобальт, у которых внутренние d-орбитали заполнены лишь частично, а следовательно, эти ионы обладают ненулевым магнитным моментом. Кристаллы из таких атомов могут быть ферромагнитными, если магнитные моменты всех атомов направлены одинаково. В кластере магнитный момент каждою атома взаимодействует с моментами других атомов, что может выстроить все моменты в одном направлении по отношению к какой-либо оси симметрии кластера. Такой кластер обладает суммарным ненулевым магнитным моментом; говорят, что он намагничен.

Магнитные свойства кластеров переходных металлов значительно отличаются от свойств массивных материалов. Кластер предоставляет возможность проследить, как изменяется магнитный момент вещества при переходе от атома к твердому телу. Значение магнитного момента изолированного атома переходного металла не совпадает с его значением в массивном образце. Это связано с появлением в массивном металле d-зоны проводимости и обменного взаимодействия. Так магнитный момент атома железа в моно- и биядерных соединениях железа составляет величину 6 μВ, в то время как магнитный момент атома железа в массивном металле составляет 2,2 μВ. Магнитные моменты атомов металла и магнитные свойства кластера зависят от числа атомов металла в кластере и изменяются в широком интервале. Так, для кластеров Fe_n магнитный момент на атом возрастает до 3,2 μВ при этом наблюдаются скачки величины момента, например, скачок около n = 55, что вероятно связано с заполнением плотно упакованного ядра. Магнитный момент М = 2,2 μВ, характерный для массивного материала достигается при n = 500. Для кластеров Ni_n наименьшие магнитные моменты наблюдались при n = 13 и 55, что опять соответствует магическим числам плотнейшей упаковки. Однако при изменении размера кластера следует принимать во внимание и электронные свойства кластера, и наличие блуждающего магнетизма. Так, уменьшение размера кластера приводит не только к увеличению магнитного момента, но и к возникновению магнитного момента у кластеров немагнитных металлов. Кластеры Fe_n с достаточным числом атомов интересны также с точки зрения другого магнитного свойства — суперпарамагнетизма, когда суммарный магнитный момент кластера меняет свое направление под действием тепловых флуктуации.

Реакционная и каталитическая способность

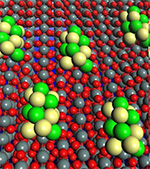
Наличие размерных эффектов в электронных и структурных свойствах наноструктур означает, что их реакционная способность по отношению к газообразным молекулам также отличается от реакционной способности массивного металла, причем в тем большей степени, чем меньше размер частиц. Первые доказательства такой зависимости получены в ходе каталитических исследований, показавших, что скорости множества реакций, катализируемых металлическими наночастицами, изменяются в том же диапазоне величин, в котором изменяются их электронные и структурные свойства. Каталитические реакции, как правило, протекают на поверхности катализатора. Исходные вещества вначале адсорбируются, мигрируют и превращаются, а образующиеся продукты затем десорбируются. Эффективность катализатора зависит от согласованного взаимодействия всех стадий процесса, а его элементарные реакции могут по-разному зависеть от размера частиц металла. Поэтому активность катализатора принято относить к единице поверхности. Эта величина, называемая удельной каталитической активностью, определяется химическим составом, размером кристаллитов, а также структурой граней, выходящих на поверхность, нарушениями в их строении и наличием всевозможных дефектов. Для более глубокого понимания каталитической активности необходимо знать число адсорбированных частиц и число атомов металла, участвующих в каталитическом процессе. Каталитические свойства нанесенных частиц могут сильно отличаться от свойств массивных металлов, поэтому не исключена возможность возникновения новых маршрутов каталитических процессов. В связи с этим можно предположить, что преимущества наноструктур, приготовленных стандартными методами, как высокоселективных катализаторов зачастую оказываются нереализованными. Это может быть обусловлено широким распределением частиц по размерам и их укрупнением в процессе работы катализатора. В нанесенных металлических катализаторах, полученных промышленным синтезом, включающим стадии пропитки гранул носителя раствором соединения активного металла, последующего прокаливания и восстановления, как правило, нет сильного взаимодействия между частицами металла и поверхностью носителя, что приводит к статистическому распределению частиц по размерам. Отсутствие сильного взаимодействия способствует также спеканию наночастиц и потери ими своих каталитических способностей.

Исследование квантовой кинетики самосборки наносистем атомов 3d-переходных металлов (Fe, Co, Ni)

Контролируемая самосборка наноразмерных частиц

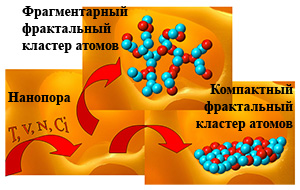
В настоящее время нанотехнология занимается поиском методов контроля процессов самосборки наноразмерных частиц для дальнейших практических нужд.

Таким образом нанотехнология ставит перед исследователем следующие вопросы:

1. Каким образом можно контролировать данный процесс?
2. Манипулирование какими параметрами системы сделают процесс самосборки системы управляемым?

Нанотехнология второго поколения

Параметр квантового запутывания — η

η = 0 — Квантово-запутанное (qs) состояние, названное моделью «слабо-коррелированного состояния».

η = 1 — Квантово-запутанное (qe) состояние, названное моделью «сильно-коррелированного состояния».

Влияние основных внешних параметров, таких как температура, количество частиц и объем в настоящее время хорошо изучено, но достаточно надежного способа управления свойствами вещества так и не найдено. Но нам также известно, что существуют внутренние параметры, которые могут дать исследователю такую возможность. Таким образом, поиск путей влияния на внутренние параметры системы становится весьма перспективным направлением, и исследования в области нанотехнологий переходят на качественно новый уровень, называемый нанотехнологией второго поколения.

Основным внутренним параметром может быть параметр квантового запутывания — η, который переключает состояния межатомного взаимодействия.

Метод Монте-Карло

Для осуществления компьютерного эксперимента на кафедре физической и коллоидной химии Алтайского государственного университета была разработана модель, позволяющая исследовать кинетику процесса самоагрегации нанокластеров переходных металлов.

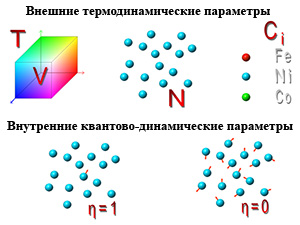
Одним из наиболее адекватных проблеме описания квазиравновесной эволюции наносистем является метод Монте-Карло. В этом методе исключается понятие траекторного движения структурных единиц, и точно учитываются процессы термостатистической стохастичности процессов. Он позволяет учитывать некоторые внешние параметры, такие как T, V, N, C_i, а также является легко адаптируемым для квантово-статистических исследований.

В данной модели метод Монте-Карло адаптируются к моделированию неравновесных процессов самосборки наносистем в заданном наноскопическом объёме. В работе использован алгоритм, предложенный Метрополисом, который был модифицирован нами для учёта двух предельных типов квантово-статистической коррелированности корпоративного движения атомов.

Первый тип представляет собой модель сильно-коррелированного состояния, ансамбль частиц в которой описывается сильно-коррелированной волновой функцией, обуславливающей стохастическое смещение на каждом шаге только одного атома на фоне фиксированной конфигурации остальных атомов.

Второй сценарий представляет собой модель слабо-коррелированного состояния атомов наночастицы, ансамбль атомов которой описывается мультипликативной (полностью факторизованной) волновой функцией, что реализуется в виде одновременного случайного блуждания всех атомов.

Определение вероятности перехода системы в новое энергетическое состояние

Проведение компьютерного эксперимента включает в себя несколько этапов.

1. На первом этапе моделирования формируется начальное конфигурационное состояние системы. Для этого задается нанообъем ограничивающий перемещение частиц.
2. На втором этапе объем полученного пространства заполняется необходимым количеством атомов, распределение которых по координатам в заданном нанообъеме осуществляется случайным образом. После этого включается процесс стохастического перемещения атомов. Выбор направления перемещения атомов осуществляется случайным образом, в зависимости от того, какому интервалу принадлежит вероятность, генерируемая оператором случайных чисел. В случае, когда выбранный элемент объема окажется занятым другим атомом, перемещения не происходит и производится операция повторного выбора направления движения.
3. На третьем этапе производится вычисление энергии наносистемы.
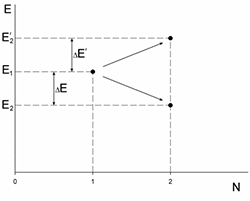
4. На четвертом этапе производится сравнение внутренней энергии нанокластера с его эго энергией до момента случайного перемещения атомов. Данный этап можно проиллюстрировать с помощью рисунка. Если система на первом шаге цепи Маркова находится в конфигурационном состоянии обладающем энергией E₁, то на втором шаге цепи она с определенной долей вероятности может оказаться в конфигурационном состоянии обладающем энергией E₂ или E'₂. Таким образом, если происходит понижение термодинамического потенциала системы, то ей приписывается новое конфигурационное состояние. В противном случае производится генерация случайного числа в интервале (0;1) и производится его сравнение с величиной больцмановского фактора. Если она оказывается больше сгенерированного числа, то система переходит в состояние с более высокой энергией. Если же этого не происходит, то ансамблю приписывается исходное конфигурационное состояние.

Внутренняя энергия описывается в нашей модели поверхностью потенциальной энергии связи (ППЭС) заданной в парном приближении. Энергия связи ε_ij рассчитанная методом орбитально-оболочечного функционала плотности для получения аналитического вида аппроксимировалась феноменологическим потенциалом Морзе.

ε — значение потенциала при равновесном расстоянии R₀;
ω — частота колебаний связи;
μ — приведенная масса.

Список рекомендуемой литературы

1. Многоуровневое строение, физико-химические и информационные свойства вещества / С.А. Безносюк [и др.]. Томск: Изд-во НТЛ, 2005. 264 с.
2. Безносюк С.А., Гришко М.С. Компьютерное моделирование методом Монте-Карло процессовформирования кластеров никеля в нанопорах материалов. М: ООО «Интерконтакт Наука», «Ультрамелкозернистые и наноструктурные материалы-2008», Перспективные материалы – Специальный выпуск (7), июнь, 2009, 388 c.
3. Гусев А.И. Нанокристаллические материалы: методы получения и свойства. Екатеринбург: УрО РАН, 1998. 199 с.
4. Рит М. Наноконструирование в науке и технике. Введение в мир нанорасчета. Москва-Ижевск: НИЦ Регулярная и хаотическая динамика, 2005. 160 с.
5. Сергеев Г.Б. Нанохимия; учеб. пособие. М.: КДУ, 2006. 336 с.
6. Хокни Р., Иствуд Дж. Численное моделирование методом частиц / пер. с англ.; под ред. Р.З. Сагдеева и В.И.  Шевченко. М.: Мир, 1987. 640 с.
7. Крокстон К. Физика жидкого состояния. Статистическое введение; пер. с англ.; под ред. А.Г. Башкирова, Н.В. Вдовиченко. М.: Мир, 1978. 400 с.
8. Физика простых жидкостей. Экспериментальные исследования / под ред. Г. Темперли; пер. с англ.; под ред. А.З. Голика. М.: Мир, 1973. 400 с.
9. Еремеев С.В. Эффективные многочастичные межатомные потенциалы в молекулярно-динамическом моделировании // Известия вузов. Физика. 2005. №6. С. 82–90.
10. Камилов И.К., Муртазаев А.К., Алиев Х.К. Исследование фазовых переходов и критических явлений методами Монте-Карло // Успехи физических наук. 1999. №7. С. 773–795.
11. Гулд Х., Тобочник Я. Компьютерное моделирование в физике; в 2 т.; пер. с англ. М.: Мир, 1990. – 2 т.
12. Хеерман Д.В. Методы компьютерного эксперимента в теоретической физике; пер. с англ. В.Н. Задкова ; под ред. С.А. Ахманова. М.: Наука,1990. 175 с.
13. Соболь И.М. Численные методы Монте-Карло. М.: Наука. Гл. ред. физ.-мат. лит, 1973. 312 с.
14. Tomar V. Accelerating the molecular time steps for nanomechanical simulations: Hybrid Monte Carlo method // J. Appl. Phys. 2007. Vol 101. P. 103512.1 – 9.
15. Yang S., Knickelbein M.B. Photoionization studies of transition metal clusters: Ionization potentials for Fe_n and Co_n // J. Chem. Phys. 1990. Vol 93. P. 1533–1546.
16. Longo R.C., Noya E.G., Gallego L.J. A density-functional study of the structures, binding energies and total spins of Ni–Fe clusters using nonlocal norm-conserving pseudopotentials and the generalized gradient approximation // The Journal Of Chemical Physics. 2005. Vol 122. P. 1–5.
17. Castro M., Jamorski C., Salahub D.R. Structure, bonding, and magnetism of small Fe_n, Co_n and Ni_n clusters, n < 5 // Chemical Physics Letters. 1997. Vol 271. P. 133–142.
18. Locatelli M., Schoen F. Minimal interatomic distance in Morse clusters // Journal of Global Optimization.2002. Vol 22. P. 175–190.
19. Vinko T., Neumaier A. New bounds for Morse clusters // J. Glob. Optim. 2007. Vol 39. P. 483–494.
20. Cox H., Johnston R.L., Murrell J.N. Empirical Potentials for Modeling Solids, Surfaces, and Clusters // Journal of Solid Stale Chemistry. 1999. Vol 145. P. 517–540.
21. Frenkel D., Smit. B. Understanding Molecular Simulation: from algorithms to applications. Academic press, 2002. 638 p.
22. Binder K., Landau P. David. A Guide to Monte Carlo Simulations in Statistical Physics, Second Edition. Cambridge: University Press, 2005. 443 p.