Плавление наночастиц
Наука о строении вещества переживает новый этап развития с начала 80-х годов прошлого века. Поворотным стало открытие функционального структурного уровня целостной организации наноматериалов в диапазоне нанометровых расстояний (10−10–10−7 м), лежащего над функциональным структурным уровнем атомов (пикометровый диапазон (10−12–10−10 м)).
Согласно определению, строение объекта — это целостная организация его функциональных структурных уровней. Каждый структурный уровень задается устойчивыми функциональными связями объекта, существенными для его целостности и тождественности с самим собой в специфических процессах взаимодействия с окружающим миром. Моноструктурный объект имеет целостную организацию на одном функциональном уровне. Строение мультиструктурного объекта задается двумя и более уровнями.
Мультиструктурные частицы имеют специфические физические, химические и информационные свойства. Кроме обычной способности к обмену энергией и веществом мультиструктурные наноматериалы могут участвовать в информационных процессах. Они имеют функции памяти, самоорганизации и адаптации.
Пограничное положение мультиструктурных частиц позволяет предположить, что законы их строения должны быть более сложными, переходными между квантово-химическими законами атомного строения и физико-химическими законами фазового строения вещества.
Вместе с тем, экспериментально обнаруженные уникальные свойства структур вещества в наномире указывают на то, что специфика их строения отличается от квантового строения молекул или классического строения фаз.
Рассмотрение экспериментальных данных и реакций атомов, кластеров и наночастиц различных элементов периодической системы позволяет сформулировать определение: размерные эффекты в химии — это явление, выражающееся в качественном изменении физико-химических свойств и реакционной способности в зависимости от количества атомов или молекул в частице вещества, происходящее в интервале менее 100 атомно-молекулярных диаметров.
Принято различать два типа размерных эффектов: собственный, или внутренний, и внешний. Внутренний эффект связан со специфическими изменениями в объемных и поверхностных свойствах, как индивидуальных частиц, так и получаемых в результате их самоорганизации ансамблей. Внешний эффект является размерно зависимым ответом на внешнее поле или действие сил, независимых от внутреннего эффекта.
Температура плавления — температура, при которой кристаллическая структура твёрдой фазы исчезает и заменяется неупорядоченным состоянием — жидкой фазой.
Температуру плавления нужно рассматривать как функцию размера частицы и ее геометрии.
Изменение температуры плавления с уменьшением размера образца были замечены давно, но из-за несовершенства приборов того времени не возможно было исследование частиц, имеющих размеры порядка нанометра. И работы в этом направлении перестали быть актуальными. Однако с развитием инструментальной базы к этому вопросу вернулись. Первые экспериментальные работы стали появляться в начале 90-х годов (Goldstein и Echer 1992, Shi 1994).
Изменение свойств
Наиболее заметные изменения физико-химических свойств наблюдаются в интервале от 1 до 10 нм.
Для металлов важно появление металлических свойств в зависимости от размера частицы. Так, для кластеров ртути постепенный переход металл—изолятор имеет место при N = 20 и N = 102 атомов.
Кинетические особенности химических процессов на поверхности наночастиц
Для адсорбированных на поверхности наночастиц реагентов химическая реакция не может рассматриваться как процесс в бесконечном объеме с постоянной средней плотностью (концентрацией) молекул. Это связано с тем, что размер поверхности наночастиц мал и сопоставим с размерами частиц реагентов. В подобных системах кинетика бимолекулярной химической реакции является кинетикой в ограниченном объеме и отличается от классической.
Для описания кинетики процессов на поверхности наночастиц можно также использовать метод Монте-Карло, или метод статистических испытаний. Это метод решения математических задач при помощи моделирования случайных процессов и событий. Фактически здесь аппарат теории вероятности применяется для решения прикладных задач с помощью ЭВМ. Число молекул реагентов на поверхности каждой наночастицы невелико, и расчеты не очень трудоемки.
Магнитные свойства
Особенности магнитных свойств наночастиц связаны с дискретностью их электронных и фононных состояний. Одной из таких особенностей является осцилляционная зависимость восприимчивости наночастиц парамагнитных металлов от напряженности магнитного поля. Кроме того, по причине малых размеров парамагнетизм Кюри может заметно перекрывать парамагнетизм Паули. Так, например, магнитная восприимчивость наночастиц Li диаметром 3,2 нм в области высоких температур соответствует парамагнетизму Паули, а в области низких температур подчиняется закону Кюри. Размерная зависимость восприимчивости обнаружена на частицах Se и Te размером от 1 до 1000 нм: уменьшение частиц Se приводит к росту диамагнетизма, тогда как магнитная восприимчивость Te изменяется в противоположном направлении из-за увеличения орбитального парамагнетизма Ван Флека.
Катализ
На поверхности катализатора исходные вещества вначале адсорбируются, мигрируют и превращаются, а образующиеся продукты затем десорбируются. Эффективность катализатора зависит от согласованного взаимодействия всех стадий процесса, а его элементарные реакции могут по-разному зависеть от размера частиц металла. Для более глубокого понимания каталитической активности необходимо знать число адсорбированных частиц и число атомов металла, участвующих в каталитическом процессе.
Одним из развиваемых в последнее время подходов к изучению каталитической активности является нанесение частиц металла на тонкие пленки различных оксидов. Подобные исследования позволяют подходить к решению проблемы, связанной с внутренними размерными эффектами и природой носителя. Изучено влияние размера частиц никеля(Ni11, Ni20, Ni30) на процесс диссоциации оксида углерода. На частицах Ni30 по сравнению с Ni11 и Ni20 ассоциативная десорбция идет более активно. Опыты с мечеными оксидами 13C 16O и 12C 18O показали наличие в частицах никеля разных мест адсорбции и десорбции, определяемых числом атомов никеля в кластере и их различными электронными свойствами.
Каталитическое окисление монооксида углерода изучено на монодисперсных частицах платины. Показано, что каждая частица платины Ptn (8 ≤ n ≤ 20), нанесенная на пленку оксида магния активна при определенной температуре в интервале 150–160 K. Установлено, что изменение размера кластера на один атом, например, при переходе от частицы Pt14 к Pt15 увеличивает активность реакции в три раза. Активность кластеров связана с изменением морфологии и энергии взаимодействия граничных орбиталей молекулы кислорода и с электронным состоянием кластера.
Оптические спектры
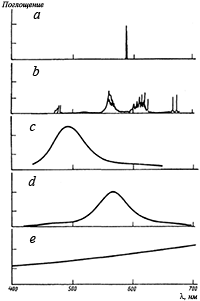
a — D-линия атома натрия,
b — кластер Na3,
c — кластер Na8,
d — наночастица натрия, 2R < 10 нм,
e — тонкая пленка натрия толщиной 10 нм
Рисунок иллюстрирует изменения оптических свойств от атома натрия до твердого компактного натрия. Зависимость изменений этих свойств сложная. Атом натрия имеет хорошо разрешенный дублет D-линии с λ = 589,0 и 589,6 нм (рис. а). Эти линии соответствуют переходу из основного состояния 2s1/2 к первым возбужденным состояниям 2p3/2 и 2p1/2. С ростом кластера исчезают индивидуальные линии и появляются одиночные широкие полосы, хотя оптический спектр дает информацию об индивидуальных особенностях своей структуры (рис. b). В оптических спектрах кластера из 8 атомов натрия уже наблюдается одиночная широкая линия (рис. c). Аналогичную линию будет иметь и кластер, состоящий из 105–106 атомов. Картина на рис. d относится к поглощению большого кластера в матрице из соли хлористого натрия. Если твердый натрий получить в виде пленки (рис. e), то в видимой области спектр становится бесструктурным.
Применение наночастиц
Применение наночастиц
- Катализаторы
- Машиностроение
- Микроэлектроника
- Медицина
- Авиапромышленность
В настоящее время нанотехнологии все более широко используются в химической промышленности, как катализаторы или носители более дорогостоящего катализатора. Наночастицы золота активны в низкотемпературном горении, окислении углеводородов и гидрировании ненасыщенных соединений. В машиностроительной отрасли, как материал при сварке металлов и сплавов, имеющих высокие температуры плавления, а также для получения сплавов с высокими температурами плавления, производство лопаток для реактивных двигателей. В микроэлектронике, для производства печатных плат. В медицине проблема применения нанотехнологий заключается в необходимости изменять структуру клетки на молекулярном уровне, т.е. осуществлять «молекулярную хирургию» с помощью наноботов. Ожидается создание молекулярных роботов-врачей, которые могут «жить» внутри человеческого организма, устраняя все возникающие повреждения, или предотвращая возникновение таковых. Манипулируя отдельными атомами и молекулами, наноботы смогут осуществлять ремонт клеток. В авиапромышленности, производство композиционных материалов, позволяющих уменьшить вес конструкции и увеличить прочность. Эти технологии основаны на том, что наночастицы имеют совершенно иные физико-химические свойства, чем у кристаллических или аморфных материалов.
Цель лекции
Исследование зависимости температуры плавления от химического состава, размера и формы наночастиц.
Термодинамическая модель
С позиции термодинамики переход из твёрдого состояния в жидкое с увеличением температуры начинается с появления на поверхности наночастицы бесконечно малого жидкого слоя, когда её ядро ещё остаётся твёрдым. Подобное плавление обусловлено поверхностным натяжением, отражающим взаимодействие жидкое-твёрдое и изменяющим энергию системы.
Рассмотрим сначала изолированную частицу малого размера. Строгое термодинамическое рассмотрение искривлённой поверхности конденсированной фазы методом Гиббса приводит к уравнению Гиббса-Толмена-Кенига-Баффа:
где σ и R — поверхностное натяжение и радиус частицы, δ — постоянная Толмена, равная по порядку величины толщине поверхностного слоя. В общем случае уравнение (1) не разрешимо в явном виде. В теории для его решения принимается условие R >> δ, что позволяет в числителе и знаменателе правой части правой части (1) избавиться от выражений в скобках. В этом случае элементарное интегрирование приводит к следующей известной формуле:
где σ(∞) — поверхностное напряжение плоской поверхности. Можно, однако, показать, что общее решение уравнения (1), когда δ не зависит от R, представимо в виде:
Численные оценки показывают, что по сравнению с (3) приближённая формула (2) даёт чрезмерно завышенные значения. Из проведённых вычислений следует, что решение (3) без существенной потери точности может быть заменено асимптотическим выражением:
Формула (4) является достаточно точной; в худшем случае отклонения от формулы (3) при малых радиусах (R ~ δ) не превышает 5%. Для сравнения отметим, что при тех же условиях для формулы (2) отклонение составляет более 20%. Поверхностное натяжение твёрдого тела определяется межатомными связями и пропорционально температуре плавления. В связи с этим для температуры плавления получим:
где Tm(∞) — температура плавления массивного образца, V — молярный объём, L — толщина первой координационной сферы, Cp — молярная теплоёмкость при постоянном давлении.
Фононная модель
Зависимость температуры плавления наночастиц металлов от размера объясняется также на основе критериев, предложенных Линдеманом. Согласно представлениям Линдемана, кристалл плавится, когда среднеквадратичное смещение атомов ⟨⟨u⟩⟩ в кристалле становится больше доли внутриатомных расстояний. Увеличение температуры ведет к возрастанию амплитуды колебаний. При некоторой температуре они становятся достаточно большими, разрушают кристаллическую решетку и твердое тело начинает плавиться. Атомы поверхности связаны слабее, и в реальных условиях это может приводить к большим амплитудам колебаний при той же температуре, чем у атомов, находящихся в объеме частицы. Этот эффект можно описать как среднеквадратичное смещение атомов на поверхности частицы ⟨⟨u²S⟩⟩ и внутри частицы ⟨⟨u²V⟩⟩. Доля поверхностных атомов в сферических наночастицах размером 3 нм достигает приблизительно 50%, и их колебания сильно влияют на критерий Линдемана. Это обстоятельство и было использовано для описания зависимости температуры плавления наночастиц от их размера без применения представлений термодинамики.
Модель, рассматривающая понижение температуры наночастиц с уменьшением их размера, развита в работе. Для описания свойств наночастиц предложено уравнение:
где Tm(r) и Tm(∞) — температуры плавления (K) нанокристалла и компактного металла соответственно; d — высота монослоя атомов в кристаллической структуре; f — параметр, учитывающий размер и форму наночастицы; α — отношение среднеквадратичных смещений на поверхности и в объёме наночастицы (значения α, в большинстве случаев, меняется от 2 до 4).
Влияние матрицы
Некоторые нанокристаллические частицы являются материалами, в которых один металл включён в другой. В подобных случаях точка плавления частицы может, как понижаться, так и повышаться по сравнению с компактным материалом при изменении размера частицы. Так, например, когда нанокристаллы индия включены в железо, температура плавления наночастиц понижается, но при их включении в алюминий - увеличивается. Важно отметить, что уравнение (6) можно применять для описания процессов, связанных с увеличением температуры плавления при уменьшении размера частицы, если значение параметра α < 1. В соответствии с равенством α=⟨⟨u²S⟩⟩/⟨⟨u²V⟩⟩ это имеет место, когда амплитуды колебаний атомов на поверхности меньше, чем в объёме. Такое положение может возникнуть в случае сильного взаимодействия атомов, расположенных на поверхности, с материалом основной матрицы.
В рамках практической работы «Моделирование процессов плавления наночастиц» слушатели курса смогут в компьютерном эксперименте изучить методику расчета температуры плавления наночастиц на основе фононной модели, с помощью программы, позволяющей учесть форму наночастицы и ее размер.
Методы анализа наноразмерных материалов
Электронная микроскопия
В 30-х годах прошлого века, когда немецкие ученые Эрнст Кнолл и Макс Руска создали микроскоп, в котором вместо света использовали поток электронов. В основе электронного микроскопа лежит утверждение Луи де Бройля о дуализме, согласно которому, движущийся электрон одновременно является и частицей, и электромагнитной волной. Устройство оптического и электронного микроскопов имеет много общего.
В электронной микроскопии выделяют два основных метода исследования.
Растровая электронная микроскопия — метод анализа поверхности образцов при сканировании выделенного участка сфокусированным потоком ускоренных электронов. В результате взаимодействия с образцом, электроны попадают на детектор, и изображение считывается с поверхности образца «строка за строкой», а затем выводится на монитор компьютера. Этим методом можно получить информацию не только о рельефе поверхности и размере частиц, но и о химическом составе образца и кристаллических фазах, находящихся на поверхности. Современные растровые микроскопы позволяют получать изображения поверхности образца с разрешением до 1 нм.
Просвечивающая электронная микроскопия — метод анализа внутренней микроструктуры и размера ультратонких, прозрачных для ускоренных электронов, образцов тоньше 100 нм, который осуществляется облучением исследуемой области потоком ускоренных электронов. Изображение, полученное таким образом, является как бы «тенью» образца, увеличенная копия которой проецируется на флуоресцентный экран или фотопленку. По этому изображению можно судить о форме и размерах частиц, из которых состоит образец. Благодаря тому, что ускоренные электроны взаимодействуют с электронными оболочками атомов изучаемого вещества, с помощью электронного микроскопа получают дифракционную картину от упорядоченной структуры атомов, из которой можно извлечь информацию о кристаллических фазах. Современные электронные микроскопы высокого разрешения, обладающие очень точной системой фокусировки, позволяют визуализировать картину распределения электронной плотности в образце, то есть практически «увидеть» ряды отдельных атомов!
Атомно-силовая микроскопия
Атомно-силовая микроскопия позволяет анализировать на атомном уровне структуру самых разных твердых материалов — стекла, керамики, пластиков, металлов, полупроводников. Измерение можно проводить не только в вакууме, но и на воздухе, в атмосфере любого газа и даже в капле жидкости. Этот метод незаменим и для исследования биологических объектов.
Микрозонд представляет собой тонкую пластинку-консоль (ее называют кантилевером, от английского слова “cantilever” — консоль, балка). На конце кантилевера расположен острый шип (радиус закругления от 1 до 10 нм). При перемещении микрозонда вдоль поверхности образца острие шипа приподнимается и опускается, очерчивая микрорельеф поверхности, подобно тому, как скользит по грампластинке патефонная игла. На выступающем конце кантилевера (над шипом) расположена зеркальная площадка, на которую падает и от которой отражается луч лазера. Когда шип опускается и поднимается на неровностях поверхности, отраженный луч отклоняется, и это отклонение регистрируется фотодетектором. Данные фотодетектора используются в системе обратной связи, которая обеспечивает постоянную силу давления острия на образец. Пьезоэлектрический преобразователь может регистрировать изменение рельефа образца в режиме реального времени. В другом режиме работы регистрируется сила взаимодействия острия с поверхностью при постоянном положении шипа над образцом. Микрозонд обычно делают из кремния или нитрида кремния. Разрешающая способность метода составляет примерно 0,1–1 нм по горизонтали и 0,01 нм по вертикали. Смещая зонд по горизонтали, можно получить серию рельефов и с помощью компьютера построить трехмерное изображение.
При использовании атомно-силовой микроскопии не требуется, чтобы образец проводил электричество. Благодаря этому атомно-силовая микроскопия нашла широкое применение для анализа биологических объектов — кристаллов аминокислот, белков, клеточных мембран и многого другого.
Сканирующая туннельная микроскопия
Сканирующий туннельный микроскоп (СТМ) исторически является предшественником всех сканирующих зондовых микроскопов. СТМ был первым устройством, давшим реальные изображения поверхностей с атомным разрешением.
Принцип его действия заключается в измерении туннельного тока. Электрический ток может возникать в различных средах и иметь различную природу. Например, потоки ионов в электролите, поток заряженных частиц в ускорителе, электрический ток в проводах. Туннельный ток возникает между зондом и образцом, если приложить напряжение, несколько меньше, чем нужно для отрыва электронов из образца. В силу законов квантовой механики, вероятность выхода электрона с поверхности все же существует. Главная в данном случае особенность туннельного тока — экспоненциальная зависимость от расстояния между поверхностью образца и зондом.
Технически работа микроскопа происходит следующим образом. Между острием иглы и образцом прикладывается рабочее напряжение порядка 1 В, и при подводе острия к образцу примерно на 0,5–1,0 нм электроны с образца начинают «туннелировать» через зазор к острию. Игла движется над поверхностью и сканирует образец. На основании данных о величине тока в каждой точке восстанавливается рельеф поверхности.
Чтобы обеспечить протекание тока, и образец, и острие должны быть проводниками или полупроводниками. Изображений диэлектриков СТМ дать не может. Останавливаясь на физических принципах, положенных в основу работы СТМ, отметим, что процесс туннелирования электронов происходит при перекрытии волновых функций атомов острия сканирующей иглы и поверхности.
Экспоненциальная зависимость туннельного тока от расстояния придает СТМ очень высокую чувствительность: считается, что с помощью туннелирования можно измерять объекты порядка 0,001 нм.
Основное приложение СТМ — это измерения рельефа. Именно благодаря своей чрезвычайно высокой чувствительности СТМ способен формировать изображения поверхностей с точностью до сотых долей нанометра по вертикали и с точностью до размеров атомов по горизонтали.
На основе общего принципа работы СТМ (принципа измерения туннельного тока) разработан ряд методик, которые применяются для исследований различных материалов и образцов.
- Режим постоянной высоты.
В режиме постоянной высоты острие иглы перемещается в горизонтальной плоскости над образцом, а ток туннелирования изменяется. Исходя из данных о величинах тока туннелирования, промеренных в каждой точке сканирования поверхности образца, строится образ топографии. - Режим постоянного тока.
В режиме постоянного тока СТМ используется система обратной связи для поддержания постоянного тока путем подстройки высоты сканирующего устройства над поверхностью в каждой точке. Например, когда система детектирует увеличение туннельного тока, то она подстраивает напряжение, прикладываемое к пьезоэлектрическому сканирующему устройству, так, чтобы отвести острие дальше от образца. В режиме постоянного тока визуализация топографии осуществляется на основании данных о величине вертикальных перемещений сканирующего устройства. Если система поддерживает ток туннелирования постоянным в пределах нескольких процентов, то расстояние между острием и образцом будет постоянным с погрешностью в несколько сотых долей нанометра.
У каждого режима есть преимущества и недостатки. Режим постоянной высоты более быстрый, так как системе не приходится передвигать сканирующее устройство вверх и вниз, но при этом можно получить полезную информацию только с относительно гладких поверхностей. В режиме постоянного тока можно с высокой точностью измерять нерегулярные поверхности, но измерения занимают больше времени.
Очевидно, что от качества иглы и радиуса ее острия будет зависеть качество получаемого скана и разрешающая способность СТМ. Промышленные зонды имеют радиус острия иглы порядка нескольких атомных слоев.
Список ремомендуемой литературы
- Косевич А.М. Теория кристаллической решётки: учеб. для физ. и физ.-техн. Спец. Вузов. Х. : Вища шк., 1988. 304 с.
- Мокроусов Г.М. Перестройка твердых тел на границах раздела фаз. Томск: Изд-во ТГУ, 1990. 230 с.
- Лозовик Ю.Е. Исследование ориентационного плавления и термодинамических свойств наночастицы методом молекулярной динамики// ФТТ. 2002. Т.44. вып.1. c. 22–26.
- Коротков П.К. Размерный эффект контактного плавления металлов // ПЖТФ. 2006. Т. 32.В. 2. c. 28–32.
- Безносюк С.А. Квантовая реология и конфайнмент электронов в наноструктурах кояденсированного состояния // Изв. вузов. Физика. 1994. Т. 37. №8. c. 60–68.
- Shi F.G. Size dependent thermal vibrations and melting in nanocrystals// J. Mater. Res. 1994. V.9. N5. P. 1307–1313.
- Бейдер Р. Атомы в молекулах: Квантовая теория: Пер. с англ. М.: Мир, 2001. 532 с.
- Татевский В.М. Атомы в молекулах. Квантово-химические модели // Журн. физ. химии. 1995. Т. 69. 2. c. 298–303.
- Губин С.П. Химия кластеров. Наука, Москва, 1987. 263 с.
- Лифшиц В.Г. Процессы на поверхности твердых тел. Владивосток: Дальнаука, 2003. 704 с.
- Суздалев И.П. Нанокластеры и нанокластерные системы// Успехи химии. 2001. Т. 70. с. 203–240.
- Zhao M. Melting and surface melting of low-dimensional In crystals // Solid State Communications. 2004. V. 130. N1. P. 37–39.
- Магомедов М.Н. О влиянии формы поверхности нанокристаллов на их свойства// Поверхность. 2005. № 1. c. 94–104.
- Магомедов М.Н. О зависимости поверхностной энергии от размера и формы нанокристалла// ФТТ. 2004. Т. 46. №5. c. 924–937.
- Магомедов М.Н. О поверхностной энергии нанокристалла// ЖФХ. 2005. Т. 79. №5. c. 829–838.
- Петров Ю.И. Физика малых частиц. М.: Наука, 1982. 360 с.
- Нагаев Э.Л. Малые металлические частицы// УФН. 1992. Т. 162. №9. c. 49–54.
- Коверда В.П. // Физика металлов и металловедение. 1981. Т. 51. № 3. c. 569-573.
- Wautelet M. Size effect on the melting (or disordering) temperature of small particles //Solid State Communications, 1990 V. 74, №11, P. 1237–1239.
- Магомедов М.Н. О поверхностном давлении для ограненного нанокристалла// ПЖТФ. 2005. Т. 31. В.1. c.24-33.
- Магомедов М.Н. Об изменении "поверхностного" давления в нанокристалле с температурой // Теплофизика высоких температур. 2005. Т. 43. №6. c. 870–879.
- Захаров Ю.А. Химия твёрдого тела; ГОУ ВПО «Кемеровский государственный университет». Кемерово: Кузбассиздат, 2006. 124 с.
- Брандт Н.Б. Электроны и фононы в металлах М.: Изд-во МГУ, 1990.
- Гусев А.И. Нанокристаллические материалы: методы получения и свойства. Екатеринбург: УрО РАН, 1998, 200 с.
- Оно С. Молекулярная теория поверхностного натяжения. М.: Изд-во иностр. Лит., 1963. 348 c.
- Роулинсон Дж. Молекулярная теория капиллярности. М.: Мир, 1986. 460 c.
- Помогайло А.Д., Наночастицы металлов в кластерах. Х., Москва, 2000. 672 c.
- Schmid G. Preparation and characterization of Langmuir monolayers and Langmuir–Blodgett films of nanosized Au55-clusters // J. Chem. Soc., Dalton Trans. 1998, 1077.
- Базулев А.Н. Применение термодинамической теории возмущений к расчету межфазного натяжения малых объектов // ЖФХ. 2002. Т. 76. В. 11. c. 2073–2077.
- Ниженко В.И. Поверхностное натяжение жидких металлов и сплавов. М.: Металлургия, 1981. 208 с.
- Гиббс Дж. Термодинамика. Статистическая механика. М.: Наука, 1982. 584 с.
- Бандин А.Е., Безносюк С.А. Термодинамическая и фононная модели плавления сферических наночастиц 3d-переходных металлов// Третья всероссийская конференция по наноматериалам НАНО 2009. Екатеринбург 20–24 апреля 2009 г. Екатеринбург: Уральское изд-во, 2009. 800 с.: ил.

