Полиаморфные переходы и нанострутуры льда
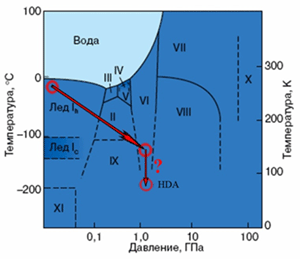
Получение HDA в реальном эксперименте [1] происходит под воздействием высокого давления и криогенных температур на низкоплотные кристаллические фазы льда (кубическую и гексагональную) как показано на фазовой диаграмме. Видно, что этот переход можно формально представить как переход в два этапа. На первом этапе полиморфный переход типа Ih→VI, где VI — плотная кристаллическая фаза льда. На втором этапе аморфизация шестой фазы.
В этой связи следует привести основные сведения, полученные экспериментально и теоретически, касающиеся полиморфных превращений под действием высоких давлений и низких температур, а именно переход из низкоплотной гексагональной фазы Ih в высокоплотную кристаллическую фазу VI.
Экспериментально (рентгенографическим и методом рамановской спектроскопии) доказано, что во всех кристаллических и аморфных льдах, а также в жидкой воде существует фиксированная структурная единица, состоящая из пяти молекул воды с тетраэдрической конфигурацией и называемая пентамером Вольрафена [2].
Методами молекулярной динамики показано, что взаимное расположение пентамеров Вольрафена для локальных структур льдов Ih и VI имеет вид, как показано на рис. 2а.
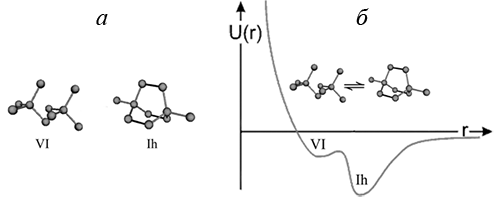
Рис. 2. Локальные структуры пентамеров Вольрафена кристаллических льдов Ih, VI (а) и профиль энергетической поверхности для локального превращения Ih ↔ VI (б) [1, 4] Экспериментально установлено [3, 4], что на рентгенограммах кристаллического льда VI и высокоплотного аморфного льда во второй координационной сфере наблюдается пик на расстоянии 3.4 Å (рис. 3). Это расстояние соответствует изогнутым водородным связям между двумя пентамерами Вольрафена. Молекулярно-динамические эксперименты так же отмечают появление этого пика за счет уменьшения пиков первой и второй координационных сфер характерных для локальной структуры гексагонального льда Ih (рис. 3).
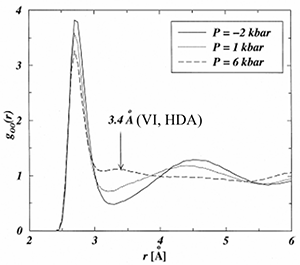
Рис. 3. Функция радиального распределения атомов кислорода локальной структуры Ih, VI, HDA по результатам МД моделирования [1] - Предполагается, что полиаморфные превращения обусловлены локальным перестроением пентамеров Вольрафена по типу (Ih ↔ VI). Методами молекулярной динамики показано, что для этих двух конфигураций пентамеров Вольрафена в профиле энергетической поверхности существует два минимума (рис. 2б) [1].
Известно, что аморфный лёд ниже 135 K может существовать в двух различных аморфных фазах. Более тяжелую аморфную фазу назвали аморфным льдом высокой плотности АЛВП (HDA), а менее тяжелую — аморфным льдом низкой плотности АЛНП (LDA) [5]. Явление существования нескольких фаз аморфного льда было названо полиаморфизмом, а превращения между фазами полиаморфными переходами соответственно. Помимо воды, полиаморфизм характерен для Si, Ge, нанокристаллического TiO2 и других систем. Жидкости и аморфные твердые тела с сетчатой структурой подобно H2O, SiO2, GeO2, C могут рассматриваться как вещества, для которых возможны полиаморфные превращения. Параллельно с накоплением экспериментального материала много усилий направлено на развитие общей теоретической картины строения жидкого, переохлажденного и аморфного состояний, переходов между ними. В настоящее время природа явлений аморфизации кристаллического льда и полиаморфизма не вполне ясна.

Представления о существовании только прямых и изогнутых внутримолекулярных водородных связях воды, позволяет описать только полиморфные превращения типа Ih → VI, но не аморфизацию на этапе фазового перехода VI → HDA и полиаморфные превращения.
Ключевым моментом аморфизации является формирование из изогнутых энергетически не выгодных внутримолекулярных водородных связей прямых межмолекулярных водородных связей. Представления о существовании внутри- и межмолекулярных водородных связей возникают в рамках концепций термополевой динамики и квантово-полевой химии.
Концепции термополевой динамики (ТПД) и квантово-полевой химии (КПХ)
Физическое поле ≡ φ(r, t)
Электромагнитное поле
φ(E, B, t)
Фотоны
Электронное поле
ρ(r, t)
Спин-орбитали
Спиновое поле
φ(sz, t)
Спиновые волны
Термополевая динамика [6] является общей концепцией описания физических полей любой природы (электронные, электромагнитные, звуковые, спиновые и др.). В общем случае поле определяется заданием пространственной функции распределения некоторого свойства в момент времени t:
Физическое поле ≡ φ(r, t)
Так, например, в случае электронного поля φ это распределение электронной плотности, электромагнитного поля φ — это распределение векторов (E, B), спинового поля φ — это распределение спина и т.д.
Квантовое поле возникает, когда разрешенными являются не все распределения, а только некоторые из них, определяемые из решения фундаментальных уравнений квантовой теории. В результате квантовое поле определяется заданием базиса из всевозможных функций распределения:
Квантовое физическое поле ≡ {φi(r, t)}, i ∈ счетное множество
Квантами электронного поля является спин-орбитали, электромагнитного — фотоны, звукового — фононы, спинового — спиновые волны и т.д.
Квантово-полевая химия [7–10], являясь частным случаем термополевой динамики, занимается квантовой теорией электронных полей, применительно к химическим системам.
В термополевой динамике показано, что динамика физических полей включает:
Унитарную динамику операторов поля. Математическое выражение имеет следующий вид:
, (1)
, (2)
, (3)
где
— оператор уничтожения, а
— оператор рождения i-й спин-орбитали.
Унитарно-неэквивалентное отображение (представление) операторов поля в базисах квантов физических полей в физическом пространстве R3. Для электронного физического поля это электронные спин-орбитали.
Реально в эксперименте наблюдаются кванты физического поля, а не операторы их рождения-уничтожения. Второй пункт определяет, какие кванты φi будут наблюдаться в эксперименте. Т.е. на уровне операторов поля решение уравнения (1) универсально при заданных условиях, однако наблюдаемая реализация движения (динамики) физического электронного поля будет разной в зависимости от множества квантов спин-орбиталей φi, т.к. средние наблюдаемые физических величин являются функционалами от базисного набора спин-орбиталей (E̅ = E̅[{φi}]). Другой набор даст другое среднее значение. Говорят, что базисный набор φi задает электронную структуру физического поля электронов. Перестроение набора φi означает электронный фазовый переход, если это перестроение осуществляется унитарно-неэквивалентным преобразованием. Т.к. уравнение (2) содержит в себе высшую производную второго порядка по координатам, то решение (1) допускает сингулярности (топологические дефекты спин-орбиталей) двух типов (рис. 4).
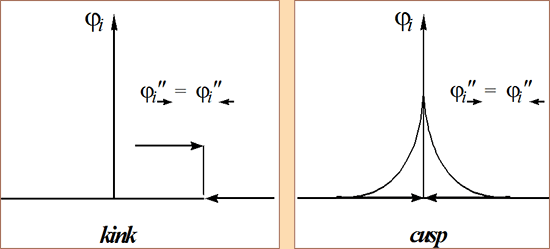
В электронных подсистемах в адиабатическом приближении присутствуют только каспы, расположенные на ядрах. Базисы спин-орбиталей электронов неэквивалентны, когда содержат различное число каспов.
В методах ССП МО спин-орбитали в базисе делокализованы по всем ядрам — они предельны по числу каспов (рис. 5а). В методах ОВС (обобщенных валентных связей), наоборот, спин-орбитали базиса предельно локализованы (рис. 5б). Образующиеся базисы спин-орбиталей в этих методах различаются по числу каспов, поэтому являются унитарно-неэквивалентными.
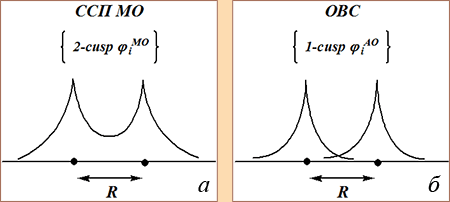
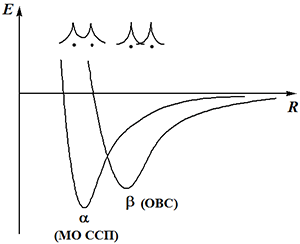
Согласно пункту 2, в термополевой динамике, электронные структуры с унитарно-неэквивалентными спин-орбиталями различаются средними значениями наблюдаемых физических величин, в частности, спектрами энергий стационарных состояний (в том числе и основных состояний). В адиабатическом приближении для рассмотренного на рис. 5 случая при изменении параметра R получим две реализации поверхности потенциальной энергии (рис. 6).
Методы расчета внутримолекулярной водородной α-связи и межмолекулярной водородной β-связи
Внутримолекулярной водородной связи (сокращенно α-связь) соответствуют делокализованные по всей системе молекулярные спин-орбитали, а межмолекулярной водородной связи (сокращенно β-связь) — спин-орбитали локализованные на каждой молекуле в отдельности. Кратко рассмотрим методы и результаты расчетов энергии связей на основе изложенных выше представлений об электронном строении вещества. Для расчета параметров внутримолекулярных водородных связей использовался метод МО ССП в базисе с поляризационными d-орбиталями 6-31 G*, а для расчета параметров межмолекулярных водородных связей использовался метод нелокальных функционалов плотности в варианте орбитально-оболочечных функционалов плотности.
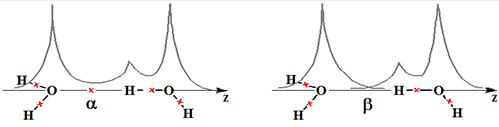
Внутримолекулярная ((Н2О)2)
водородная α-связь
Расчет производился неэмпирическим методом в базисе с поляризационными d-орбиталями 6-31G*
Межмолекулярная (2(Н2О))
водородная β-связь
Метод нелокальных функционалов плотности ООФП
Основные формулы метода нелокальных функционалов плотности в варианте ООФП приведены ниже. Детали метода и назначение всех величин можно найти в [7–10].
Энергия основного состояния наночастиц:
Неэлектростатическая энергия m-ой частицы:
Потенциальная энергия:
Кинетическая энергия:
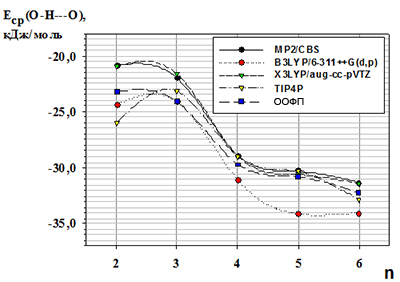
- Метод MP2 с базисом CBS (Xantheas S.S., et. al. // J. Chem. Phys. 2002, V.116 (4), P. 1493.);
- Метод функционала плотности, B3LYP с базисом 6-311++G(d,p) (Tawa G.J., et. al. // J. Chem. Phys. 1998, V.109, P. 4852);
- Метод гибридного функционала плотности, X3LYP с базисом aug-cc-pVTZ (Julius T. Su, et. al. // J. Phys. Chem. A 2004, V.108, P. 10518);
- Метод с использованием эмпирического потенциала TIP4P, параметризованного по свойствам объёмного вещества (Wales D.J., et. al. // Chem. Phys. Lett. 1998. V.286. P. 65).
В аморфном льде для расчета внутримолекулярных водородных связей были рассмотрены кластеры воды с количеством молекул от 2 до 13. Как показано на рис. 7 результаты расчетов хорошо согласуются с расчетными данными полученными наиболее точными квантово-химическими методами для кластеров с числом молекул воды от 2 до 6. Кроме того, они выходят на предел насыщения для числа молекул больше или равно шести. Это позволяет взять в качестве среднего потенциала внутримолекулярной водородной связи потенциал гексагонального кластера воды, который представлен на рис. 8а.
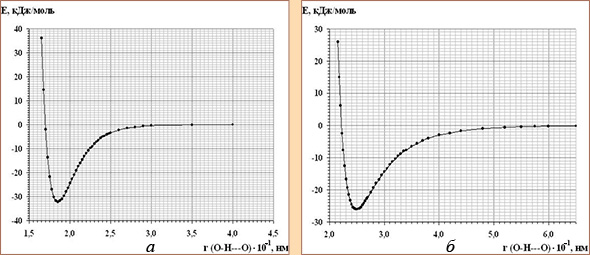
На рис. 8б представлен аналогичный потенциал для межмолекулярной водородной связи рассчитанный методом нелокальных функционалов плотности. Равновесные длины и энергии связей равны соответственно
- Eα(O—H—O) = −32.2 кДж/моль,
Lα(O—H—O) = 0.185 нм; - Eβ(O—H—O) = −26.1 кДж/моль,
Lβ(O—H—O) = 0.249 нм.
На основании полученных данных на следующем этапе в [14] предложена кристаллохимическая модель переходов кристаллических модификаций фаз льда в аморфные фазы высокой и низкой плотности под действием высоких давлений и криогенных температур.
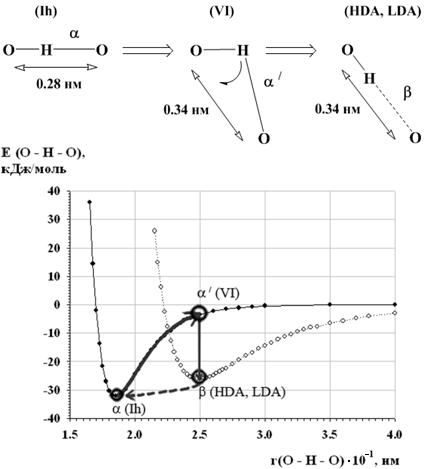
В области криогенных температур при атмосферном давлении лед существует в кристаллической гексагональной модификации. При увеличении давления до 1 ГПа происходит деформация гексагональной структуры льда Ih с образованием аморфной фазы высокой плотности. Локальная структура HDA фазы соответствует структуре кристаллического льда VI. На уровне пентамеров Вольрафена эта стадия отвечает поворотно-сдвиговой деформации пентамеров по типу Ih→VI с изгибом водородных связей. На рис. 9 этому переходу соответствует перемещение вдоль жирной стрелки на кривой, соответствующей внутримолекулярной водородной связи. К существующей модели нами сделано следующее дополнение. На следующей стадии происходит разрыв изогнутых внутримолекулярных водородных связей с поворотом атома водорода на линию, соединяющую два атома кислорода. В результате появляется благоприятная соответствующая минимуму на кривой межмолекулярной водородной связи конфигурация. На этой стадии происходит скачкообразный переход с листа внутримолекулярной водородной α-связи на лист межмолекулярной водородной β-связи.
Подробнее ознакомиться с математическим аппаратом модели, особенностями ее реализации и основными результатами можно в монографии [15].
Литература
- Mishima O. Melting ice’ I at 77 K and 10 kbar: a new method of making amorphous solids / O. Mishima, L.D. Calvert, E. Whalley // Nature. – 1984. – Vol.310. – Р. 393–395.
- Walrafen G.E. Raman spectral studies of water structure / G.E. Walrafen // J. Chem. Phys. – 1964. – Vol.40. – P. 3249–3256.
- Canpolat M. Local structural heterogeneities in liquid water under pressure / M. Canpolat, F.W. Starr, A. Scala, Е.M. Reza Sadr-Lahijany, O. Mishima, S. Havlin, H.E. Stanley // Chem. Phys. Lett.– 1998. – Vol.294. – P. 9–12.
- Okhulkov A.V. X-ray scattering in liquid water at pressures of up to 7.7 kbar: Test of a fluctuation model / A.V. Okhulkov, Yu.N. Demianets, Yu.E. Gorbaty // J. Chem. Phys. – 1994. – Vol.100. – P. 1578–1588.
- Mishima O. The relationship between liquid, supercooled and glassy water / O. Mishima, E. Stanley // Nature. – 1998. – Vol.396. – Р. 329–335.
- Умэдзава Х. Термополевая динамика и конденсированное состояние / Х. Умэдзава, Х. Мацумото, М. Татики; пер. с англ. – М.: Мир, 1985. – 504 с.
- Beznosyuk S.A. Approximating quasi-particle density functional calculations of small active clusters: Strong electron correlation effects / S.A. Beznosyuk, B.F. Minaev, R.D. Dajanov, Z.M. Muldakhmetov // Int. J. Quant.Chem. – 1990. – Vol.38. – Р. 779–797.
- Beznosyuk S.A. Density functional calculation of transition metal cluster energy surfaces / S.A. Beznosyuk, R.D. Dajanov, A.T. Kuljanov // Int. J. Quant. Chem. – 1990. – Vol.38. – Р. 691–698.
- Beznosyuk S.A. Informative energetic structure and electronic multistability of condensed state / S.A. Beznosyuk, B.F. Minaev, Z.M. Muldakhmetov // J. Mol. Struct. (Theochem). – 1991. – Vol.227. – Р. 125–129.
- Мулдахметов З.М. Теория электронного строения молекул (Новые аспекты) / З.М. Мулдахметов, Б.Ф. Минаев, С.А. Безносюк. – Алма-Ата: Наука, 1988. – 216 с.
- Paul J.B. Direct measurement of water cluster concentrations by infrared cavity ringdown laser absorption spectroscopy / J.B. Paul, C.P. Collier, R.J. Saykally, J.J. Scherer, A. O’Keefe // J. Phys. Chem. A. – 1997. – Vol.101. – P. 5211–5214.
- Волошин В.П. Структурная неоднородность аморфного льда низкой плотности и ее влияние на динамику молекул воды / В.П. Волошин, Е.А. Желиговская, Г.Г. Маленков, Ю.И. Наберухин // Журн. структ. химии. – 2001. – Т.42. – №5. – С. 948–957.
- Mishima O. Reversible first-order transition between two H2O amorphs at ~0.2 GPa and ~135 K / O. Mishima // J. Chem. Phys. – 1994. – Vol.100. – P. 5910–5912.
- Beznosyuk S.A. Structure of solid amorphous phases of water and capture of molecules СН4, Н2 in multistructures of an ice / S.A. Beznosyuk, A.A. Perezhogin // Hydrogen Materials Science and Chemistry of Carbon Nanomaterials // NATO Security through Science Series A: Chemistry and Biology, 2006. Р. 293–302
- Жуковский М.С. Теоретические основы компьютерного наноинжиниринга биомиметических наносистем / М.С. Жуковский, С.А. Безносюк, А.И. Потекаев, М.Д. Старостенков. – Томск: Изд-во Научно-Техническая Литература. – 2011. 236 с.

