Эволюция мультистабильных нанотрансформеров в пространстве (ESI)

Для описания движения наночастиц, как изменения их внутренней атомной структуры и внешней структуры химических и физических связей с другими наночастицами требуется определить их состояние движения. Так как функциональный уровень структур наночастиц отвечает за целостность вещества в физико-химических процессах обмена механической и тепловой энергией, а также обмена информацией с окружающей средой, то свойства вещества имеют три основных количественных критерия: энергию (U), энтропию (S) и информацию (I). Поэтому процесс можно представить как перемещение изображающей наночастицу точки в обобщенном пространстве критериев движения, как это показано на рисунке. Для описания движения наночастицы вещества требуется использования не только динамических наблюдаемых, таких как энергия, импульс, угловой момент, но и кинематических наблюдаемых — информации и энтропии.

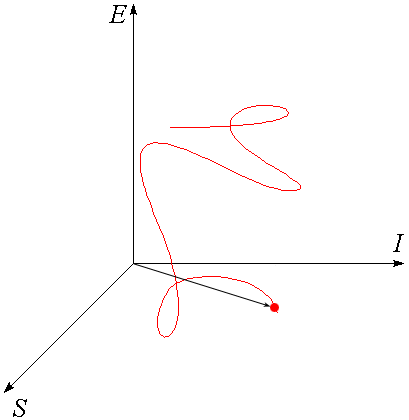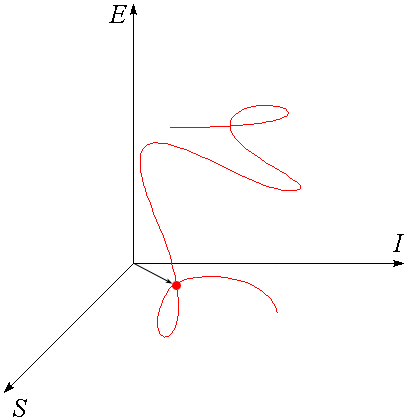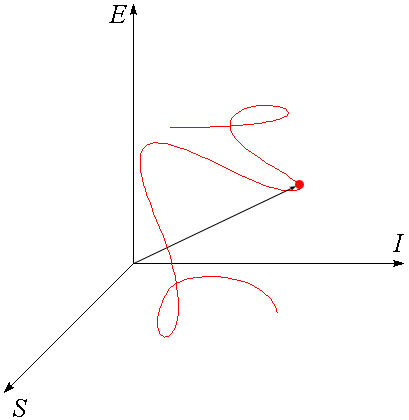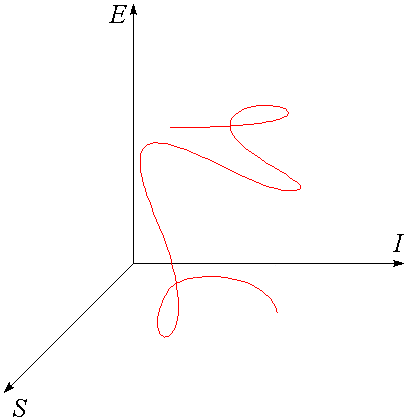
Дадим феноменологическую трактовку воображаемому пространству критериев (U, S, I). По шкале внутренней энергии объекта измеряется масса механического движения его частей в физическом пространстве. Для неё известна универсальная формула Эйнштейна E = m₀ c² , где m₀ — масса покоя объекта, а c — скорость света в вакууме. По шкале энтропии измеряется хаос теплового движения частей объекта в физическом пространстве. Для неё известна универсальная формула Больцмана S = k ln(W_s), где k — константа Больцмана, а W_s — число квантовых микросостояний движения, неразличимо реализующих наивероятное макросостояние объекта как целого в условиях его теплового равновесия. Величина информации измеряет сложность устройства объекта по универсальной формуле Хартли: I = log₂(W_i), где W_i — число различимых модификаций структур (форм движения) объекта при заданном уровне внутренней энергии и энтропии.