Квантовая теория движения наноэлектромеханических систем (НЭМС) конденсированного состояния

Безносюк С. А., Жуковский М. С.

Изложена теория движения в конденсированном состоянии квантовых электромеханических плазмоидных наноботов. Механизм функционирования плазмоидного нанобота связан с квантовым обменом спутанной парой (e⁻e⁺)-плазмоида между наночастицей и квантово-полевой электронной системой конденсированного состояния. Дана интерпретация работы (e⁻e⁺)-плазмоида, как квантового аналога топливного элемента на борту НЭМС нанобота. Электрические и магнитные силовые поля (e⁻e⁺)-плазмоида управляют квантовым движением НЭМС нанобота. Это обуславливает отклик нанобота на внешние воздействия и позволяет построить физические инструменты для управления самодвижением НЭМС нанобота в материале. В статье показано существование двух механизмов релаксационного самодвижения плазмоидного нанобота в конденсированной среде: механизма конверсии внутренней квантово-механической энергии нанобота в электрическую энергию квантового (e⁻e⁺)-плазмоида и механизма конверсии электрической энергии квантового (e⁻e⁺)-плазмоида в механическую работу по перемещению нанобота в материале. Эти механизмы задают дискретный процесс манипуляций и транспорта НЭМС нанобота в материале. Даны оценки времени, смещения, сил и мощности при транспорте НЭМС нанобота.

Ключевые слова: НЭМС, нанобот, плазмоидный солитон, физика конденсированного состояния, квантово-механические системы, открытые квантовые системы, квантовая релаксация, моделирование

The theory of motion in the condensed state of quantum electromechanical plasmoid nanobots is stated. The mech-anism of functioning of the plasmoid nanobot is caused by the exchange of quantum entangled pair (e⁻e⁺)-plasmoid between nanoparticle and quantum electronic field of the condensed state. The interpretation of (e⁻e⁺)-plasmoid as the quantum analogue of the fuel cell on board NEMS nanobot is suggested. Quantum motion of the NEMS nanobot is controlled by (e⁻e⁺)-plasmoid electric and magnetic force fields. This causes the response of nanobots to external influences and allows one to build the physical tools to control the NEMS nanobot self-movement in the material. In the paper it is shows that there are two mechanisms for the plasmoid nanobot relaxation self-motion in condensed matter: the mechanism of conversion of nanobot internal quantum-mechanical energy into quantum (e⁻e⁺)-plasmoid electrical energy and the mechanism of conversion of the quantum (e⁻e⁺)-plasmoid electrical energy into mechanical work on nanobot movement in the material. These mechanisms specify discrete process of manipulation and transport NEMS nanobot in the material. Estimation of time, displacement, force and power in the transport of NEMS nanobot are given.

Key words: NEMS, nanobot, plasmoid solitary wave, condensed state physics, quantum mechanical systems, open quantum systems, quantum relaxation, modeling

Введение

В ряде работ нового направления нанобиодизайна рассматриваются бионические прототипы нанороботов – наноботов, которые могут найти применение в области инжиниринга новых функциональных материалов. В них отмечается, что в основу создания и контроля бионических наноботов можно положить известные в биологии механохимические процессы самосборки и самоорганизации молекулярных химических систем. Типичным является механизм конверсии электронно-колебательно-вращательных возбуждений молекул или нанокристаллов в механическую работу по перемещению бионических наноботов и формированию супрамолекулярных структур типа: «ключ-замок», «хозяин – гость». Исследователями отмечается, что наряду с достоинствами бионических наноботов, такими как скорость и селективность их ферментативно-каталитических манипуляций, у них есть существенные недостатки: малая мощность и медленность выполнения работы. Прежде всего, недостатки касаются механохимических молекулярных моторов [1, 2].

Вместе с тем, развивается электромеханическое направление в создании наноботов на базе достижений микроэлектромеханических систем (МЭМС). Создание адаптивных к внешним условиям среды кибернетических наноустройств и приборов является наиболее приоритетной целью инжиниринга следующего по миниатюризации поколения наноэлектромеханических систем (НЭМС). Особую значимость это имеет для резкого повышение эффективности производства, переработки и утилизации энергии, информации, материалов, а также создания принципиально новых наносистем с высокими ресурсами мощности и интеллекта [3, 4].

Важно подчеркнуть принципиальные различия между свойствами механохимических и электромеханических наноботов. Существует мнение, что для систем, содержащих менее тысячи атомов свойства механохимических и электромеханических наноботов должны конвергировать. Так как с точки зрения квантовой механики разницы между квантовохимическими и квантовоэлектродинамическими системами в этой области уже нет. Но это заблуждение. Потому что кроме пространственных размеров существенную роль для функций наноботов играют временные рамки выполнения операций. Атомно-молекулярные системы химии по временным характеристикам процессов в области малых квантовых систем не вполне эквивалентны квантовым электродинамическим системам ядер и электронов в физике конденсированного состояния. Химическая атомно-молекулярная структура материала является устойчивой лишь для медленных воздействий на квантовую электродинамическую систему ядер и электронов в диапазоне частот химических и фо-тохимических превращений. Квантовая электродинамическая система конденсированного состояния устойчива также в областях сверхбыстрых воздействий, когда атомно-молекулярная (медленная, адиабатическая) све6рхструктура материала уже утрачивает физический смысл. Нехимические квантовые механизмы движения НЭМС наноботов должны стать основными в развитии инжиниринга биомиметических наносистем [5]. Особенности квантовых механизмов движения электромеханических наноботов, базирующихся на быстром импульсном обмене электрон-дырочными (e⁻e⁺)-плазмоидами с материалом являются предметом изучения в данной работе.

Основы теории квантовой динамики и кинетики электромеханических наноботов

Механизмы самосборки, самоорганизации и самодвижения открытых систем связаны между собой процессом квантовой релаксации [5]. Согласно теореме Фока – Крылова [6], для процесса квантовой релаксации необходимо, чтобы динамическая система (наночастица) была квантово-механической системой с конечным числом степеней свободы и дискретным спектром энергии, а диссипативная система (конденсированное состояние), напротив, должна быть квантово-полевой системой с бесконечным несчётным числом степеней свободы и непрерывным спектром энергии. Только в этом случае существуют механизмы процесса диссипации энергии, ведущие к квантовой релаксации наночастицы, как основного механизма её спонтанного движения.

С другой стороны, в рамках теории квантово-полевой химии конденсированного состояния [7] показано, что только в квантово-полевых моделях физики конденсированного состояния определены механизмы самосборки и самоорганизации открытых компактных квантово-механических наночастиц. Эти частицы способны спонтанно трансформировать конфигурационные пространства динамических переменных x_n и алгебраические структуры статистических операторов D_nT(t) состояний движения [8, 9]. Квантово-полевые механизмы лежат в основе, как процессов самосборки и самоорганизации, так и процессов самодвижения в форме квантовой релаксации открытой наночастицы в диссипативной системе конденсированного состояния [10, 11].

Будем исходить из того, что наночастица с конечным числом степеней свободы является открытой квантовой динамической системой, находящейся в контакте с диссипативной системой конденсированного состояния. Она обменивается с диссипативной системой частицами (δN_n ≠ 0) и энергией (δE_n ≠ 0). К частицам относятся электроны и ядра. Не останавливаясь на анализе [12] проблемных аспектов общей квантовой теории необратимости движения конечных квантовых систем, рассмотрим основную логическую схему описания, применимую к открытой наночастице, эволюционирующей в диссипативной системе конденсированного состояния.

Система «наночастица + диссипативная система конденсированного состояния» является замкнутой и описывается статистическим оператором (матрицей плотности) чистого квантового состояния D. Они зависят от времени согласно квантового уравнения Лиувилля:

$iћ∂D(t)/∂t = [H, D]$ ,(1)

где Н — гамильтониан, включающий кроме гамильтониана Н_n наночастицы и гамильтониана диссипативной системы Н_Т, гамильтониан их взаимодействия — Н_nT:

$Н = Нn + НТ + НnT$ .(2)

В основном приближении необратимости для системы «наночастица + диссипативная система конденсированного состояния» статистический оператор D(t) представим в виде произведения статистических операторов смешанных квантовых состояний наночастицы D_nT(t) и среды D_T [6]:

$D(t) ~ Dзап(t) = DTDnT(t)$ .(3)

Здесь D_T — независящий от времени статистический оператор термодинамической равновесной диссипативной системы конденсированного состояния. В (3) D_nT(t) — статистический оператор наночастицы, обменивающейся энергией и частицами с термостатом. В приближении необратимости (3) уравнение эволюции наночастицы в смешанном квантовом состоянии приобретает вид кинетического уравнения [6]:

$∂DnT(t)/∂t = L[хn(t), DnT(t), <yT>]$ ,(4)

где L – кинетическая функция квантового Лиувиллиана, зависящая от операторов динамических физических величин х_n(t) и статистического оператора D_nT(t) наночастицы, а также от средних значений физических величин 〈y_T〉, диссипативной системы термостата, вычисленных в термодинамическом равновесном состоянии. Величины 〈y_T〉 определяют интенсивные параметры процесса релаксации наночастицы в смешанном квантовом состоянии.

Если в начальный момент времени наночастица находится в неравновесном термодинамическом состоянии, то с течением времени, подчиняясь кинетическому уравнению (4), она стремится в равновесное термодинамическое состояние. Приближение квантовой системы наночастицы к равновесному состоянию называется процессом квантовой релаксации.

Квантовая кинетика процесса диссипативной релаксации открытой наночастицы, описываемая кинетическим уравнением типа (4), сложна. Прежде всего, форма кинетической функции Лиувиллиана L в правой части кинетического уравнения (4) зависит от сложности моделей гамильтониана взаимодействия Н_nT наночастицы с диссипативной средой конденсированного состояния [5]. С другой стороны, необходимо учитывать в ходе релаксации сложные модели процессов спонтанной трансформации внутренних кинематических параметров конфигурационного пространства динамических переменных x_n(t) и алгебраической структуры статистического оператора D_nT(t) наночастицы [8, 9]. Требуется сформулировать общий подход к решению проблем моделирования.

Рассмотрим модели квантовой релаксации наночастицы в квантово-полевой диссипативной системе конденсированного состояния детально. С этой целью подставим гамильтониан полной системы (2) и основное приближение необратимости (3) в квантовое уравнение Лиувилля (1). В результате получим следующее операторное уравнение общего вида:

$\left(i\hbar\frac{\partial D_{T}}{\partial t}\right)D_{nT} + D_{T}\left(i\hbar\frac{\partial D_{nT}}{\partial t}\right) = H_{n}D_{T}D_{nT} - D_{T}D_{nT}H_{n} + \\ H_{T}D_{T}D_{nT} - D_{T}D_{nT}H_{T} + H_{nT}D_{T}D_{nT} - D_{T}D_{nT}H_{nT}$ .(5)

В этом уравнении используем условие кинетической стационарности квантово-полевой диссипативной системы конденсированного состояния (термостата Т):

$\frac{\partial D_{T}}{\partial t} = 0$ (6)

и условия кратковременности флуктуаций статистического оператора D_T квантово-полевой диссипативной системы в форме требования коммутации статистического оператора состояния диссипативной системы с каждой компонентой гамильтониана объединённой системы «наночастица + диссипативная квантово-полевая система конденсированного состояния»:

$\left[H_{n}, D_{T}\right] = \left[H_{T}, D_{T}\right] = \left[H_{nT}, D_{T}\right] = 0$ .(7)

Тогда уравнение спонтанной и необратимой релаксации квантовой наночастицы в контакте с квантово-полевой диссипативной системой примет вид редуцированного квантового уравнения Лиувилля для статистического оператора наночастицы D_nT:

$i\hbar\frac{\partial D_{nT}}{\partial t} = \left[H_{n}, D_{nT}\right] + \left[H_{T}, D_{nT}\right] + \left[H_{nT}, D_{nT}\right]$ .(8)

Рассмотрим физический смысл трёх процессов эволюции открытой наночастицы, описываемых слагаемыми в правой части квантово-полевого кинетического уравнения Лиувилля (8).

Операторные условия замкнутости наночастицы, при нулевом обмене частицами (δN_n = 0) и энергией (δE_n = 0) с квантово-полевой диссипативной системой, имеют вид:

$\left[H_{T}, D_{nT}\right] = \left[H_{nT}, D_{nT}\right] = 0$ .(9)

В пределе замкнутой наночастицы уравнение (8) сводится к уравнению эволюции вида:

$i\hbar\frac{\partial D_{nT}}{\partial t} = \left[H_{n}, D_{nT}\right]$ .(10)

При условии консервативности изолированной наночастицы, т. е. явной независимости её гамильтониана Н_n от времени, уравнение (9) интегрируется. В рамках квантовой теории представлений показывается, что оператор-коммутатор [Н_n, D_nT] является инфинитезимальным генератором группы операторов сдвига во времени вида U_n(t) = exp(−itН_n/ћ).

Оператор U_n(t) = exp(−itН_n/ћ) — это оператор унитарно-эквивалентного преобразования статистического оператора, так как он преобразует при сдвиге времени начальное гильбертово пространство H_nT(0) состояний наночастицы в эквивалентное ему гильбертово пространство H_nT(t) в момент времени t [7].

При кратковременных в течение времени Δt флуктуациях диссипативной системы конденсированного состояния погружённая в неё наночастица становится открытой. Это определяется действием двух других операторов: L_T(Δt) = exp(−iΔtН_Т/ћ) и Λ_nT(t) = exp(−iΔtН_nT/ћ). Их инфинитезимальными генераторами являются операторы: [Н_Т, D_nT] и [Н_nТ, D_nT], соответственно. Необратимый сдвиг статистического оператора открытой наночастицы за время Δt генерируется его коммутатором с собственным гамильтонианом Н_Т квантового поля диссипативной системы конденсированного состояния и с гамильтонианом Н_nТ взаимодействия наночастицы с квантовым полем диссипативной системы конденсированного состояния.

Пара операторов L_T(Δt) и Λ_nT(Δt) сдвига времени математически описывает квантовую эволюцию любой открытой релаксирующей наночастицы. Вместе с тем, в каждом случае необходимо строить физическую модель механизма реализации квантово-полевого процесса релаксационного движения конкретного типа наночастиц. В частности, этот квантово-полевой подход применим к описанию физических механизмов необратимой квантовой релаксации открытых компактных наноэлектромеханических систем наноботов.

На Рис. 1 показано как открытая плазмоидная наночастица создается оператором L_T(Δt) унитарно-неэквивалентным преобразованием одного листа гильбертова пространства H^N закрытой N-электронной наночастицы (Рис.1а) в триплет сопряжённых гильбертовых подпространств {H^N−1; H^N; H^N+1} пространства Фока (Рис.1b) открытого нанобота с переменным числом электронов {N−1, N, N+1}. Для описания нанобота, как системы «ядра + электроны + плазмоид (e⁻e⁺)», требуется использовать три смежных листа Фоковского пространства N−1, N, N+1-электронных состояний. Зарядово-сопряжённые квантовые состояния |N−1〉 «катиона» нанобота (с e⁺-дыркой плазмоида) и квантовые состояния |N+1〉 «аниона» нанобота (с e⁻-электроном плазмоида) спутаны плазмоидной электронной парой конденсированного состояния согласно формуле:

$\left|N-1,N+1\right>=\left [\left|N-1\right>+\left|N+1\right>\right ]/\sqrt{2}$ .(11)

Вектор чистого квантового состояния электронов плазмоидного нанобота имеет вид:

$\left|N-1,N,N+1\right>=C_N\left|N\right>+C_{N\pm 1}\left [\left|N-1\right>+\left|N+1\right>\right ]/\sqrt{2}$ ,(12)

при выполнении условия нормировки для коэффициентов квантовой суперпозиции:

$\vert C_{N}\vert^{2} + \vert C_{N\pm1}\vert^2 = 1$ (13)

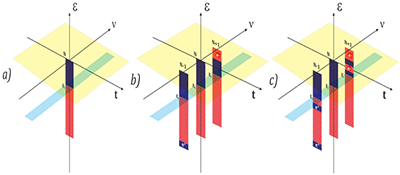
Рис.1 a) Унитарно-эквивалентное Гильбертово пространство H^N закрытой наночастицы (N-e⁻);. b) унитарно-неэквивалентный триплет {H^N−1; H^N; H^N+1} пространства Фока открытого нанобота (N-e⁻ + (e⁻e⁺)-плазмоид); неунитарно-неэквивалентный триплет {H^N−1; H^N; H^N+1} пространства Фока открытого нанобота (N-e⁻+ (e⁻e⁺)-плазмоид + (e⁻e⁺)’-плазмоид), ε – энергии одноэлектронных состояний с уровнем Ферми E_f ; υ – координата числа электронов в пространстве Фока

Оператор Λ_nT(Δt) описывает нарушение унитарности эволюции нанобота на интервале Δt за счёт того, что гамильтониан взаимодействия НnT нанобота рождает в конденсированном состоянии дополнительные квантовые флуктуации (e⁻e⁺)’-плазмоидов вблизи уровня Ферми (Рис.1c.).

Генерация (e⁻e⁺)-плазмоида формирует в пространстве материала солитонную кинематическую волну зарядовой поляризации плотности электронов нанобота (Рис. 2c). При этом солитон плазмоида имеет характерное распределение плотности избыточного положительного заряда e⁺- дырочной компоненты в окрестности ядер внутри объёма (Рис. 2b) и отрицательного избыточного заряда e⁻-электронной компоненты в межъядерных областях плазмоида (Рис. 2a). Кинематическая волна зарядовой поляризации плотности (e⁻e⁺)-плазмоида экранирует локализованную на её носителе наночастицу от остальной матрицы материала (Рис. 2d), формируя вместе с ней автономную энергонасыщенную наноэлектромеханическую систему плазмоидного нанобота.

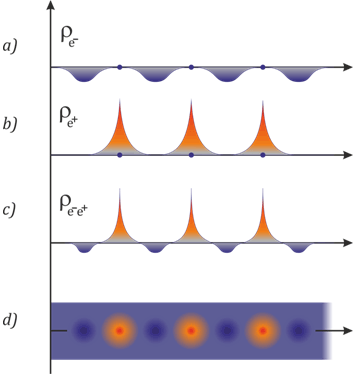
Рис.2 Распределение плотности заряда: a) электрона; b) дырки; c) кинематической волны заряда электрон-дырочного плазмоида; d) карта распределения плотности заряда (e⁻e⁺)-плазмоида.

Квантовая механика плазмоидных наноботов в адиабатическом приближении

Плазмоидный нанобот возникает из наночастицы в результате её захвата (e⁻e⁺)-плазмоидом – 2-х электронной флуктуации квантового поля электронной системы конденсированного состояния. Матрица плотности D_nT(t) n-нанобота в чистом квантово-механическом состоянии имеет вид:

$D_{nT}\left (t\right) = \Psi_{n}^*\left(r, R\vert t\right) \Psi_{n}\left(r, R\vert t\right)$ ,(14)

где совокупность координат всех электронов нанобота и приданной ему (e⁻e⁺)-плазмоидной пары обозначена буквой r, а совокупность координат ядер нанобота – буквой R.

Гамильтониан, определяющий состояние нанобота, как объединённой системы «наночастица + (e⁻e⁺)-плазмоид» можно записать формально в общем виде:

$H = T_{R} + T_{r} + V\left(r, R\right)$ ,(15)

где

$T_{R} = -\frac{\hbar^{2}}{2} \sum_{p}\frac{1}{M_{p}}\frac{\partial^{2}}{\partial R_{p}^{2}}$ (16)

– оператор кинетической энергии В ядер c номерами {p = 1,..., B}, массами {M_p} и координатами {R_p}.

$T_{r} = -\frac{\hbar^{2}}{2} \sum_{i}\frac{1}{m}\frac{\partial^{2}}{\partial r_{i}^{2}}$ (17)

– оператор кинетической энергии N электронов c номерами {i = 1,..., N−1, N, N+1}, массами m и координатами {r_i}; V(r,R) — оператор потенциальной кулоновской энергии взаимодействия между ядрами и электронами.

Волновая функция стационарного состояния наночастицы с фиксированным числом {N−1, N, N+1}электронов и c энергией Е имеет вид:

$\Psi\left(r, R\vert t\right) = \Psi\left(r, R\right)\exp\left(-\frac{iEt}{\hbar}\right)$ ,(18)

где пространственная часть Ψ(r,R) — решение стационарного уравнения Шредингера на собственные функции гамильтонианов Н = {H^N−1; H^N; H^N+1}:

$\left(H - E\right)\Psi\left(r, R\right) = 0$ .(19)

В адиабатическом приближении оператор кинетической энергии ядер T_R можно рассматривать как оператор малого возмущения и представить гамильтониан Н в виде невозмущённого гамильтониана Н₀ = T_r + V(r,R) и возмущения

$H = T_R + H_0$ .(20)

Тогда в нулевом адиабатическом приближении волновую функцию нанобота можно представить в виде произведения волновой функции ядер χ₀(R) и волновой функции электронов Φ₀(r|R)

$\Psi_{0}\left(r, R\right) = \chi_{0}\left(R\right)\Phi_{0}\left(r\vert R\right)$ .(21)

С учётом вида векторов (11-13) для электронной функции Φ₀(r|R) плазмоидного нанобота имеем:

$\Phi_{0}\left(r\vert R\right) = C_{N}\Phi_{0}^{N}\left(r\vert R\right) + C_{N\pm 1}\Phi_{0}^{N\pm 1}\left(r\vert R\right)$ ,(22)

где волновая функция спутанного (2e⁻) электронной парой плазмоида (e⁻e⁺) имеет вид симметричной суперпозиции волновых функций катионного Φ₀^N−1(r|R) и анионного Φ₀^N+1(r|R) состояний наночастицы:

$\Phi_{0}^{N\pm 1}\left(r\vert R\right) = \left(1/\sqrt{2}\right)\left[\Phi_{0}^{N - 1}\left(r\vert R\right) + \Phi_{0}^{N + 1}\left(r\vert R\right)\right]$ ;(23)

при условии нормировки когерентной суперпозиции двух базисных волновых функций нанобота:

$\vert C_{N}\vert^{2} + \vert C_{N\pm1}\vert^2 = 1$ .(24)

Волновые функции базисных стационарных состояний с числом электронов N и N±1 находятся как решения электронных стационарных уравнений Шрёдингера вида (19) при фиксированной конфигурации ядер R и числе электронов {N−1, N, N+1} в наночастице, соответственно:

$\left[H_{0}^{N} - \epsilon_{0}^{N}\left(R\right)\right]\Phi_{0}^{N}\left(r\vert R\right) = 0$ .(25)

$\left[H_{0}^{N\pm 1} - \epsilon_{0}^{N\pm 1}\left(R\right)\right]\Phi_{0}^{N\pm 1}\left(r\vert R\right) = 0$ .(26)

В (26) два листа ε₀^N±1(R) адиабатической энергетической поверхности в конфигурационном пространстве ядер R запишем через отклонения от основного листа N-электронной наночастицы ε₀^N(R):

$\epsilon_{0}^{N\pm1}\left(R\right) = \epsilon_{0}^{N}\left(R\right) + \delta\epsilon_{0}^{N\pm1}\left(R\right)$ .(27)

Для каждой конфигурации ядер R отклонения δε₀^N±1(R) – это, энергия сродства A₀(R) = δε₀^N+1(R) к электрону и энергия электронной ионизации I₀(R) = δε₀^N−1(R) нанобота в состоянии Φ₀^N(r|R), соответственно. Поэтому можно переписать (27) в виде:

$\epsilon_{0}^{N+1}\left(R\right) = \epsilon_{0}^{N}\left(R\right) + A_{0}\left(R\right)$ .(28)

$\epsilon_{0}^{N-1}\left(R\right) = \epsilon_{0}^{N}\left(R\right) + I_{0}\left(R\right)$ .(29)

В силу соотношений (22) - (29) средняя потенциальная энергия ядерной подсистемы нанобота в адиабатическом состоянии (21) с волновой функцией χ₀(R)Φ₀(r|R) при фиксированной конфигурации ядер R имеет вид:

$\epsilon_{0}\left(R\right) = \epsilon_{0}^{N}\left(R\right) + \delta\epsilon_{0}^{N,N\pm1}\left(R\right)$ (30)

где дополнительный запас энергии нанобота δε₀^N, N±1 (R) связан с захватом им спутанной (2e⁻) пары (e⁻e⁺)-плазмоида в электронной среде конденсированного состояния материала:

$\delta\epsilon_{0}^{N,N\pm1}\left(R\right) = \vert C_{N\pm1}\vert^{2}\left[A_{0}\left(R\right) + I_{0}\left(R\right)\right]/2$ (31)

Полученные соотношения (21) – (31) позволяют дать интерпретацию устройству плазмоидного нанобота, как компактной квантовой наноэлектромеханической системы, имеющей на «борту» квантовый «топливный элемент» в виде разделённой в пространстве (e⁻e⁺)-плазмоидной пары с запасом энергии – δε₀^N, N±1 (R). Солитоное распределение заряда (e⁻e⁺)-плазмоидной пары формирует в пространстве нанобота квантовые аналоги «электродов топливного элемента»: в остовной области ядер (e⁺)–«анод» и (e⁻)-«катод» во внешних для остовов межъядерных областях нанобота. Волновая функция нанобота в чистом квантовом состоянии (e⁻e⁺)-плазмоидного топливного элемента нулевом адиабатическом приближении имеет вид (23).

Квантово-кинетический процесс релаксационного движения плазмоидного нанобота в конденсированном состоянии

Выход за рамки нулевого адиабатического приближения состоит в том, чтобы искать решение Ψ уравнений (19) в виде суперпозиции двух ортогональных волновых функций вида:

$\Psi = \chi_{0}\Phi_{0} + \chi_{1}\Phi_{1}$ ,(32)

где в соответствие с Рис. 1с имеем волновую функцию спутанных флуктуацией (e⁻e⁺)’-плазмоида состояния катиона и аниона нанобота Φ₁, ортогональную как к Φ₀^N±1(r|R), так и к Φ₀^N(r|R):

$\Phi_{1}\left(r\vert R\right) = \Phi_{1}^{N\pm1}\left(r\vert R\right) = \frac{1}{\sqrt{2}}\left[\Phi_{1}^{N-1}\left(r\vert R\right) + \Phi_{1}^{N+1}\left(r\vert R\right)\right]$ .(33)

При этом коэффициенты разложения по базису электронных волновых функций Φ₀ и Φ₁ являются волновыми функциями χ₀(R) и χ₁(R) ядерной подсистемы нанобота.

В приближении малости неадиабатического возмущения нанобота 〈χ₀|χ₀〉= 1 - 〈χ₁|χ₁〉 ≈ 1 и ортогональности ядерных компонент волновых функций 〈χ₀|χ₁〉 = 0 решение уравнений (19) для волновой функции вида (32) можно найти из системы двух связанных уравнений вида:

$\left(T_{R} + \epsilon_{0}\left(R\right) - E\right)\chi_{0} = \Lambda_{00}\chi_{0} + \Lambda_{01}\chi_{1}$ ,(34)

$\left(T_{R} + \epsilon_{0}\left(R\right) + \delta\epsilon_{1}\left(R\right) - E\right)\chi_{1} = \Lambda_{10}\chi_{0} + \Lambda_{11}\chi_{1}$ .(34')

В уравнениях в правой части стоят операторы неадиабатичности, в которые входят операторы дифференцирования по координатам ядер Λ. Их стандартный вид хорошо известен [6]. Кроме того, в левой части уравнения (34) для малой добавки ядерной волновой функции χ₁ введено отклонение δε₁(R) для энергии флуктуаций заряда в состоянии состоянии Φ₁:

$\epsilon_{1}\left(R\right) = \epsilon_{0}\left(R\right) + \delta\epsilon_{1}\left(R\right)$ .(35)

Электронная «жёсткость» δε₁(R) нанобота равна половине энергии δε_|e+e−〉(R) возбуждения конденсированным состоянием дополнительной флуктуации (e⁻e⁺)’ плазмоида в наноботе:

$\delta\epsilon_1\left(R\right)=\delta\epsilon_{\left|e^+e^-\right>}\left(R\right)/2=\left[\delta\epsilon^+_1\left(R\right)+\delta\epsilon^-_1\left(R\right)\right]/2\equiv\left[A_1\left(R\right)+I_1\left(R\right)\right]/2$ .(36)

Проанализируем решение системы уравнений (34), (34’) в случае зануления правых частей уравнений. Для этого требуется однородность в конфигурационном пространстве ядер малой добавки χ₁Φ₁. Это условие выполняется, когда для каждой ядерной переменной R_p справедливо:

$\frac{\partial}{\partial R_{p}}\chi_{1}\left(R\right) \approx 0$ ,(37)

$\frac{\partial}{\partial R_{p}}\Phi_{1}\left(R\right) \approx 0$ .(38)

Складывая левые и правые части уравнений (34), (34’), умножая слева на комплексно-сопряжённую функцию χ* = (χ₀ + χ₁)* и, интегрируя по конфигурационному пространству ядер R, получим уравнение для полная средней энергии нанобота с течением времени неадиабатического процесса движения:

$\left<\chi\left(t\right)\vert T_R\vert\chi\left(t\right)\right>+\left<\chi\left(t\right)\vert\epsilon_0\left(R\right)\vert\chi\left(t\right)\right>+\left<\chi\left(t\right)\vert \delta\epsilon_1\left(R\right)\vert\chi_1\left(t\right)\right>=E\left(t\right)$ .(39)

В приближении квазистационарности в течение малых интервалов времени τ когерентного неадиабатического состояния движения с волновой функцией (32) получаем условие для полной энергии E(t) в начале (t = 0) и в конце времени жизни (t = τ) этого состояния:

$E\left(\tau\right) \approx E\left(0\right)$ .(40)

Однородность неадиабатического движения ядер нанобота обеспечивается условиями однородности ядерной волновой функции χ₁(t) в конфигурационном пространстве ядер (37) и малостью времени τ эволюции по сравнению с характерным временем изменения χ₀(t) (период одного колебания ядер). В результате этого, волновая функция χ₀(t) адиабатического движения ядер нанобота не успевает существенно измениться за время τ, а средняя кинетическая энергия ядер в течение времени τ в неадиабатическом состоянии (32) эволюции нанобота сохраняется:

$\left\langle\chi\left(\tau\right)\vert T_{R}\vert\chi\left(\tau\right)\right\rangle \approx \left\langle\chi\left(0\right)\vert T_{R}\vert\chi\left(0\right)\right\rangle$ (41)

С учётом формул (35) – (41) получаем главное для дальнейших выводов соотношение:

$\delta\epsilon_{\left| e^+e^-\right>}\approx -\left[\left<\chi\left(\tau\right)\vert\epsilon_0\left(R\right)\vert\chi\left(\tau\right)\right>-\left<\chi_0\left(0\right)\vert\epsilon_0\left(R\right)\vert\chi_0\left(0\right)\right>\right] \equiv-\delta\epsilon_0\left(\tau\right)$ .(42)

На стадии когерентной неадиабатической релаксации в состоянии Ψ = χ₀Φ₀ + χ₁Φ₁. уравнение (42) – это уравнение конверсии квантово-механической внутренней энергии нанобота δε₀(τ) в энергию δε_|e+e−〉 подзарядки спутанного с ним (e⁻e⁺)-плазмоида из электронной среды конденсированного состояния материала. Когерентно движущиеся ядра нанобота не успевают изменить свою кинетическую энергию (31) за малое время τ неадиабатической релаксации нанобота. В результате этого изменение квантово-механической энергия δε₀(τ) нанобота идёт только на «накачку» энергией δε_|e+e−〉 связанного с наноботом (e⁻e⁺) – плазмоида.

Сбой когерентности процесса переноса дополнительного заряда на «электроды квантовых топливных элементов» (e⁻e⁺) – плазмоида нанобота из квантово-полевой электронной среды конденсированного состояния вызывается тепловыми флуктуациями термополевой динамики конденсированного состояния материала [7]. В результате этого сбоя в течение ультракороткого интервала времени δτ происходит редукция волновой функции плазмоидного нанобота из неадиабатического состояния Ψ(τ) = χ₀(τ)Φ₀(τ)+ χ₁(τ)Φ₁(τ) в адиабатическое состояние Ψ₀(τ) = χ₀(τ)Φ₀(τ):

$\Psi\left(\tau\right) = \chi_{0}\left(\tau\right)\Phi_{0}\left(\tau\right) + \chi_{1}\left(\tau\right)\Phi_{1}\left(\tau\right)\quad\Rightarrow\quad\Psi_{0}\left(\tau\right) = \chi_{0}\left(\tau\right)\Phi_{0}\left(\tau\right)$ (43)

Время редукции δτ задаётся ультракоротким временем жизни неспутанной с наноботом свободной (e⁻e⁺)’-плазмоидной флуктуации в квантово-полевой электронной среде конденсированного состояния. Время жизни можно оценить из соотношения неопределённостей для времени жизни свободной квантово-полевой флуктуации с энергией δε_|e+e−〉 = δε_exc ≈ - δε₀(τ) по формуле:

$\delta\tau \approx \hbar/\left(2\delta\epsilon_{exc}\right)$ (44)

На ультракороткой по времени δτ адиабатической стадии релаксации из законов сохранения энергии и импульса следуют два уравнения квантовой физики движения плазмоидного нанобота:

$\delta E \approx \delta\epsilon_{0}\left(\tau\right) = -\delta\epsilon_{exc}$ (45)

$\mathbf{\delta P = -\delta P_{exc}}$ (46)

Уравнения (45) и (46) показывают как изменяется энергия δЕ и импульс δP плазмоидного нанобота при «выбросе» в электронную среду конденсированного состояния материала свободной флуктуации (e⁻e⁺)’-плазмоида. Из уравнения (45) видно, что на шаге релаксации за время δτ энергия плазмоидного нанобота понижается на величину унесённой освобождённой флуктуации (e⁻e⁺)’ плазмоида энергии. Из уравнения (46) следует, что за время δτ импульс нанобота, как целого, изменяется на величину «отдачи» конденсированного состояния при испускании в него свободной флуктуации (e⁻e⁺)’-плазмоида. Исходя из формулы для импульса силы, можно оценить среднюю величину модуля F силы «отдачи», приложенной за время δτ к наноботу со стороны среды:

$F = \delta P/\delta\tau$ (47)

Принимая массу испущенного свободного (e⁻e⁺)’-плазмоида равной, приблизительно, массе 2m_е пары свободных электронов, можно дать оценку для силы F. Приравняв кинетическую энергию пары свободных электронов к энергии δε_exc, получаем искомую формулу:

$F = \sqrt{2\left(2m_{e}\right)\delta\epsilon_{exc}}/\delta\tau$ .(48)

Учитывая, что масса нанобота М – это масса его ядер, в приближении равноускоренного движения без трения с нулевой начальной скоростью, можно дать оценку для максимального смещения δS центра масс автономного нанобота за время δτ действия импульса силы «отдачи»:

$\delta S = \left(F/M\right)\delta\tau^{2}/2 = \delta P\delta\tau/2M$ .(49)

Дадим с помощью формул (44)-(49) оценки физических величин мощного движения нанобота. Рассмотрим типичный пример. Пусть унесённая (e⁻e⁺)’-плазмоидом энергия составит δε_exc ~ 2.7 эВ. Прежде всего, из формулы (44) можно оценить длительность времени редукции δτ ≈ 0.1 фс. Это – субфемтосекундный процесс. Подставляя численные значения величин в (48), найдём оценку силы: F ≈ 10 нН. В предположении, что атом водорода с массой М ≈ 2000 m_e находится в состоянии плазмоидного электромеханического нанобота, по формуле (49) имеем оценку его импульсного смещения в гипотетической конденсированной среде без трения: δS ≈ 0.3 нм. Это величина порядка среднего межатомного расстояния в типичных конденсированных фазах материалов. Можно дать оценку величины мощности. При 100% КПД работа равна всей энергия δε_exc испущенного наноботом (e⁻e⁺)’-плазмоида. Мощность такого плазмоидного наноэлектромеханического мотора: N = δε_exc/ δτ. В данном примере развиваемая мощность составляет около 4 мВт.

Для точного расчёта итогового за время δτ транспортного смещения нанобота и величины мощности мотора при совершении им работы необходимо точно учесть особенности трансграничных сил взаимодействия с окружающей его матрицей материала [4, 5].

Заключение

Электромеханический плазмоидный нанобот может существовать и двигаться только в электронной среде конденсированного состояния материала. Механизм функционирования плазмоидного нанобота связан с квантовым обменом спутанной парой электронов между наноботом и квантовополевой электронной системой конденсированного состояния. Такой механизм формирования квантовых НЭМС наноботов не имеет аналога среди молекулярных механохимических наноботов.

Квантовая механика движения плазмоидного нанобота возмущается эффектами термополевой динамики флуктуаций электронной системы конденсированного состояния. Эти эффекты возмущения движения квантового плазмоидного нанобота можно отнести к форме квантового неразрушающего контроля его движения со стороны внешней подсистемы электронов конденсированного состояния. Это же предопределяет специфический квантово-кинетический процесс релаксационного движения плазмоидного нанобота в материале.

При классическом «измерении» квантового плазмоидного нанобота произойдёт редукция его волновой функции. В результате чего в материале на месте квантового плазмоидного нанобота будут обнаружены с вероятностью |C_N|², незаряженная наночастица, или, с равными вероятностями (½)|C_N±1|², катион или анион этой наночастицы. Что, косвенно, будет свидетельствовать о том, что плазмоидный нанобот существовал в квантовом состоянии до его измерения.

Адиабатическое приближение квантовой механики не является приемлемым для описания движения плазмоидного нанобота в конденсированном состоянии. Требуется учёт эффектов неадиабатичности движения ядер нанобота и флуктуационного характера термополевой динамики электронной системы конденсированного состояния материала. В статье показано, что наличие этих эффектов проявляется в существовании двух механизмов релаксационного самодвижения плазмоидного нанобота в конденсированной среде. Эти квантовые электромеханические механизмы функционирования нанобота взаимно дополняют друг друга. Первый механизм – это короткая неадиабатическая конверсия внутренней квантово-механической энергии нанобота в электрическую энергию квантового (e⁻e⁺)-плазмоидного топливного элемента. Второй механизм – это ультракороткая адиабатическая конверсия части электрической энергии «бортового» квантового (e⁻e⁺)’-плазмоидного топливного элемента в механическую работу по перемещению нанобота внутри конденсированной фазы материала.

Двух-стадийные последовательные конверсии внутренней квантово-механической энергии в электрическую энергию (e⁻e⁺)-плазмоида и конверсии электрической энергии (e⁻e⁺)-плазмоида в квантово-механическую энергию перемещения центра масс нанобота формируют двух-тактовый дискретный процесс последовательных манипуляций и транспорта НЭМС нанобота в материале. Сравнивая между собой длительности τ и δτ двух последовательных стадий квантового движения нанобота, отметим, что в масштабе фемтосекундных [5] актов внутренней плазмоидной конверсии субфемтосекундные акты плазмоидной диссипации энергии практически мгновенны. Это указывает на бифуркационый характер прерываний когерентности фемтосекундных процессов внутренней конверсии энергии плазмоидного нанобота и на сложный прерывистый характер его самодвижения. Эстафетный режим трансформаций ядерной и электронной структуры нанобота определяет его высокую изменчивость и информационный ресурс в ходе движения в конденсированном состоянии материала. Электрические и магнитные силовые поля «бортового» квантового (e⁻e⁺)-плазмоидного топливного элемента управляют квантовым движением наноэлектромеханической системы нанобота, что обуславливает проявление высокой адаптивности отклика нанобота на внешние воздействия в процессе его движения в материале. В принципе, это позволяет построить физические инструменты для управления самодвижением НЭМС нанобота.

Список литературы

Hess Н. // Science 2006. Vol. 312. P. 779.
Lund K., Manzo A. J., Dabby N., Michelotti N., Johnson-Buck A., Nangreave J., Taylor S., Pei R., Stojanovic M. N., Walter N. G., Winfree E., Yan H. //Nature 2010. Vol. 465, P. 206.
Desai T., Bhatia S. BioMEMS and Biomedical Nanotechnology BioMEMS and Biomedical Nanotechnology // III: Therapeutic Micro/Nanotechnology. — Springer, 2007. — 1856 p.
Жуковский М.С., Безносюк С.А. // Нанотехника 2013, 1(33), с. 41.
Жуковский М.С., Безносюк С.А., Потекаев А.И., Старостенков М.Д. Теоретические основы компьютерного наноинжиниринга биомиметических наносистем / Томск: Изд-во НТЛ, 2011, 236 с.
Давыдов А.С. Квантовая механика: учеб. Пособие. – 3 изд., стреотипное. – СПб.: БХВ-Петербург, 2011, 704 с.
Beznosyuk S. A., Minaev B. F., Muldakhmetov Z. M. //Computational and Theoretical Chemistry 1991. Vol. 227, P. 125.
Фомин А.С., Жуковский М.С., Безносюк С.А.// Известия вузов. Физика. 2006, Т.49. №7. С. 66.
Жуковский М.С., Безносюк С.А.// Ползуновский вестник. 2009. № 3. С. 19.
Beznosyuk S.A., // Materials Science & Engineering C. 2002. Vol.19/1-2, P. 369.
Beznosyuk S.A., Kolesnikov A.V., Mezentsev D.A., Zhukovsky M.S., Zhukovsky T.M. //Materials Science & Engineering C. . 2002. Vol.19/1-2, P. 91.
Tarasov V.E. Quantum Mechanics of Non -Hamiltonian and Dissipative Systems / Amsterdam, Boston, London, New York : Elsevier Science, 2008. – 530 p.